
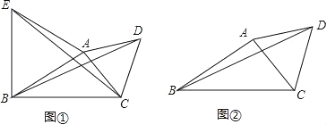
【题目】(1)如图①,△ABE,△ACD都是等边三角形,若CE=6,则BD的长=__;
(2)如图②,△ABC中,∠ABC=30°,AB=3,BC=4,D是△ABC外一点,且△ACD是等边三角形,则BD的长=__.
【答案】 6 5
【解析】试题分析:
(1)根据等边三角形的性质得到AE=AB,AD=AC,∠EAB=∠DAC=60°,则∠BAD=∠EAC,再根据三角形全等的判定方法可证得△ACE≌△ADB,根据全等的性质得出BD=CE即可;
(2)作等边三角形ABE,连接AE,则AE=AB=3,∠ABE=60°,证出∠CBE=90°,由勾股定理求出CE,即可得到结果.
试题解析:
(1)∵△ABE和△ACD是等边三角形,
∴BE=AE=AB=3,AD=AC,∠ABE=∠EAB=∠DAC=60°,
∴∠EAB+∠BAC=∠DAC+∠CAB,
∴∠BAD=∠EAC,
在△ACE和△ADB中, 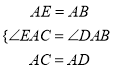 ,
,
∴△ACE≌△ADB(SAS),
∴BD=CE=6;
故答案为:6;
(2)作等边三角形ABE,连接AE,如图所示:

则AE=AB=3,∠ABE=60°,
∵∠ABC=30°,
∴∠CBE=∠ABE+∠ABC=90°,
∴CE=![]() ,
,
由(1)得:BD=CE=5;
故答案为:5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
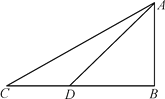
【题目】如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30,再向旗杆的方向前进16米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端A的仰角为45,请计算旗杆AB的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
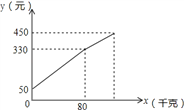
【题目】李大爷按每千克2.1元批发了一批蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降低出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)李大爷自带的零钱是 元;
(2)降价前他每千克蜜橘出售的价格是 元/千克;
(3)卖了几天,南丰蜜橘卖相不好了,随后他按每千克下降1.5元将剩下的蜜橘售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的蜜橘?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com