
【题目】如图,△ABC的三个顶点分别为A(1,2),B(1,3),C(3,1).若反比例函数y=![]() 在第一象限内的图象与△ABC有公共点,则k的取值范围是( )
在第一象限内的图象与△ABC有公共点,则k的取值范围是( )

A. 2≤k≤3B. 2≤k≤4C. 3≤k≤4D. 2≤k≤3.5
【答案】B
【解析】
根据△ABC三顶点的坐标可知,当k最小是反比例函数过点A,当k取最大值时,反比例函数与直线相切,且切点在线段BC上,由点A的坐标利用反比例函数图象上点的坐标特征可求出k的最小值,再由点B、C的坐标利用待定系数法求出直线BC的解析式,将其代入反比例函数中,令△=0即可求出k的最大值,从而得出结论.
当反比例函数过点A时,k值最小,
此时k=1×2=2;
∵1×3=3×1,
∴反比例函数图象与直线BC的切点在线段BC上,
设直线BC的解析式为y=ax+b,
∴有![]() ,
,
解得:![]() ,
,
∴直线BC的解析式为y=-x+4,
将y=-x+4代入y=![]() 中,得:-x+4=
中,得:-x+4=![]() ,
,
即x2-4x+k=0,
∵反比例函数图象与直线BC只有一个交点,
∴△=(-4)2-4k=0,
解得:k=4.
综上可知:2≤k≤4.
故答案是:2≤k≤4.


科目:初中数学 来源: 题型:
【题目】中小学时期是学生身心变化最为明显的时期,这个时期孩子们的身高变化呈现一定的趋势,7~15岁期间生子们会经历一个身高发育较迅速的阶段,我们把这个年龄阶段叫做生长速度峰值段,小明通过上网查阅《2016年某市儿童体格发育调查表》,了解某市男女生7~15岁身高平均值记录情况,并绘制了如下统计图,并得出以下结论:
①10岁之前,同龄的女生的平均身高一般会略高于男生的平均身高;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生;
③7~15岁期间,男生的平均身高始终高于女生的平均身高;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大.
以上结论正确的是( )
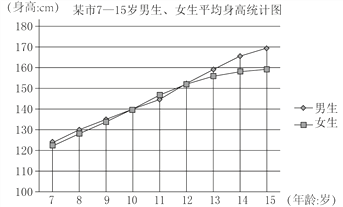
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
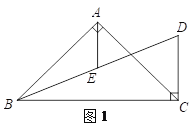
【题目】在△ABC中,AB=AC,CD⊥BC于点C,交∠ABC的平分线于点D,AE平分∠BAC交BD于点E,过点E作EF∥BC交AC于点F,连接DF.
(1)补全图1;
(2)如图1,当∠BAC=90°时,
①求证:BE=DE;
②写出判断DF与AB的位置关系的思路(不用写出证明过程);
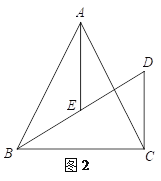
(3)如图2,当∠BAC=α时,直接写出α,DF,AE的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】育才中学开展了“孝敬父母,从家务事做起”活动,活动后期随机调查了八年级部分学生一周在家做家务的时间,并将结果绘制成如下两幅尚不完整的统计图

请你根据统计图提供的信息回答下列问题:
(1)本次调查的学生总数为 人,被调查学生做家务时间的中位数是 小时,众数是 小时;
(2)请你补全条形统计图;
(3)若全校八年级共有学生1500人,估计八年级一周做家务的时间为4小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则菱形ABCD面积为( )
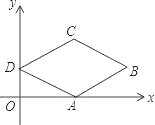
A. 8B. 16C. 24D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,射线OC在∠A0B的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“定分线”
(1)一个角的平分线______这个角的“定分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=![]() ,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
(3)如图2,若∠MPN=45°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成90°时停止旋转,旋转的时间为t秒.同时射线PM绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止.当PQ是∠MPN的“定分线”时,求t的值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com