
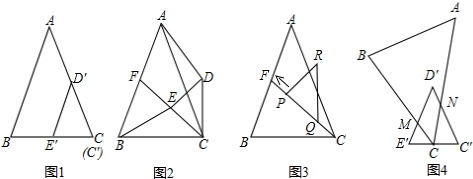
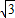 和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).
和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).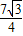 ?
?
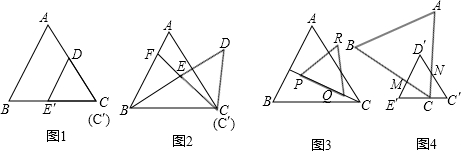
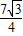 ,在△CQT中,求得QT=QC=x,RT=3-x,根据三角形面积公式可得方程
,在△CQT中,求得QT=QC=x,RT=3-x,根据三角形面积公式可得方程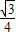 ×32-
×32-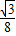 (3-x)2=
(3-x)2=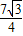 ,解此方程即可求得答案;
,解此方程即可求得答案;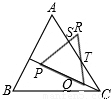
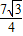 ,
,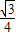 ×32-
×32-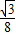 (3-x)2=
(3-x)2=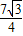 ,(6分)
,(6分)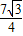 ;(7分)
;(7分) ,
, ×
× =
= .(10分)
.(10分)

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
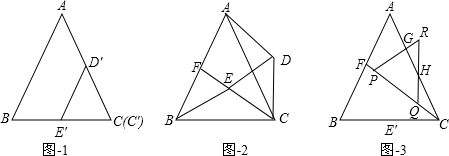 ,求y与x之间的函数解析式,并写出函数自变量x的取值范围.
,求y与x之间的函数解析式,并写出函数自变量x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
7
| ||
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com