
【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为![]() 分.前
分.前![]() 名选手的得分如下:根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为
名选手的得分如下:根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为![]() 分),现得知
分),现得知![]() 号选手的综合成绩为
号选手的综合成绩为![]() 分.
分.
序号 |
|
|
|
笔试成绩/分 |
|
|
|
面试成绩/分 |
|
|
|
(1)求笔试成绩和面试成绩各占的百分比:
(2)求出其余两名选手的综合成绩,并以综合成绩排序确定这三名选手的名次。
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
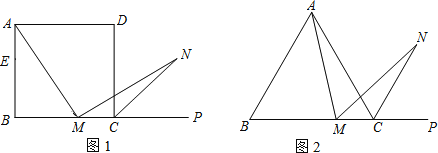
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“一起阅读,共同成长”课外读书周活动,活动后期随机调查了八年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:
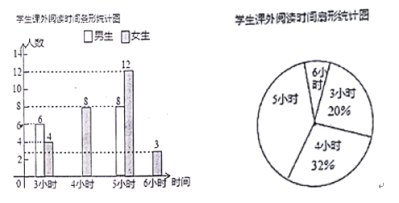
(1)本次调查的学生总数为______人,在扇形统计图中,课外阅读时间为5小时的扇形圆心角度数是______;
(2)请你补全条形统计图;
(3)若全校八年级共有学生![]() 人,估计八年级一周课外阅读时间至少为
人,估计八年级一周课外阅读时间至少为![]() 小时的学生有多少人?
小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
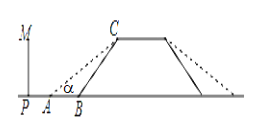
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:![]() .
.
(1)求新坡面的坡角∠CAB的度数;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O在直线AB上,作射线OC,点D在平面内,∠BOD与∠AOC互余.
(1)若∠AOC:∠BOD=4:5,则∠BOD= ;
(2)若∠AOC=α(0°<α≤45°),ON平分∠COD.
①当点D在∠BOC内,补全图形,直接写出∠AON的值(用含α的式子表示);
②若∠AON与∠COD互补,求出α的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片![]() (
(![]() )折叠,使点
)折叠,使点![]() 刚好落在线段
刚好落在线段![]() 上,且折痕分别与边
上,且折痕分别与边![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,设折叠后点
,设折叠后点![]() ,
,![]() 的对应点分别为点
的对应点分别为点![]() ,
,![]() .
.

(1)判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
(2)若![]() ,且四边形
,且四边形![]() 的面积
的面积![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD,E是线段BC上一点,N是线段BC延长线上一点,以AE为边在直线BC的上方作正方形AEFG.

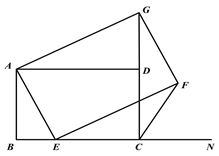
图(1) 图(2)
(1)连接GD,求证:DG=BE;
(2)连接FC,求∠FCN的度数;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=m,BC=n(m、n为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线BC的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含m、n的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请画图说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某公园准备修建一块长方形草坪,长为a米,宽为b米.并在草坪上修建如图所示的十字路,
已知十字路宽2米.
(1)用含a、b的代数式表示修建的十字路的面积.
(2)若a=30,b=20,求草坪(阴影部分)的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF
∥EB;③∠FAN=∠EAM;④△ACN≌△ABM![]() 其中正确的有 .
其中正确的有 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com