
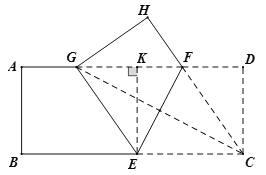
【题目】如图,将矩形纸片![]() (
(![]() )折叠,使点
)折叠,使点![]() 刚好落在线段
刚好落在线段![]() 上,且折痕分别与边
上,且折痕分别与边![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,设折叠后点
,设折叠后点![]() ,
,![]() 的对应点分别为点
的对应点分别为点![]() ,
,![]() .
.

(1)判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
(2)若![]() ,且四边形
,且四边形![]() 的面积
的面积![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)四边形![]() 为菱形,理由见解析;(2)
为菱形,理由见解析;(2)![]()
【解析】
(1)根据折叠的性质可得EC=EG,GF=CF,![]() ,由GF∥EC,可得
,由GF∥EC,可得![]() ,进一步可得GE=GF,于是可得结论;
,进一步可得GE=GF,于是可得结论;
(2)根据题意可先求得CE的长,过点E作EK⊥GF于点K,在Rt△GEK中,根据勾股定理可求得GK的长,于是FK可求,在Rt△EFK中,再利用勾股定理即可求得结果.
(1)四边形![]() 为菱形,理由如下:
为菱形,理由如下:
证明:由折叠可得:![]() ,
,![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 为菱形.
为菱形.
(2)如图,∵四边形![]() 为菱形,且其面积为
为菱形,且其面积为![]() ,∴
,∴![]() ,
,
∴![]() ,
,
过点E作EK⊥GF于点K,则EK=AB=4,
在Rt△GEK中,由勾股定理得:![]() ,
,
∴![]() ,
,
在Rt△EFK中,由勾股定理得:![]() .
.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
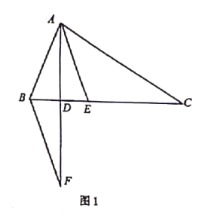
【题目】已知:![]() 中,
中,![]() 是
是![]() 的角平分线,
的角平分线,![]() 是
是![]() 的
的![]() 边上的高,过点
边上的高,过点![]() 做
做![]() ,交直线
,交直线![]() 于点
于点![]() .
.
![]() 如图1,若
如图1,若![]() ,则
,则![]() ___ ____;
___ ____;
![]() 若
若![]() 中的
中的![]() ,则
,则![]() __ ____;(用
__ ____;(用![]() 表示)
表示)
![]() 如图2,
如图2,![]() 中的结论还成立吗?若成立,说明理由;若不成立,请求出
中的结论还成立吗?若成立,说明理由;若不成立,请求出![]() .(用
.(用![]() 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60![]() m的点D(点D与楼底C在同一水平面上)出发,沿斜面坡比为i=1∶
m的点D(点D与楼底C在同一水平面上)出发,沿斜面坡比为i=1∶![]() 的斜坡DB前进30 m到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30 m到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,其坡比i=1∶![]() ,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25 m,与亭子距离CE=20 m.小丽从楼房顶测得点E的俯角为45°,求楼房AB的高.
,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25 m,与亭子距离CE=20 m.小丽从楼房顶测得点E的俯角为45°,求楼房AB的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为![]() 分.前
分.前![]() 名选手的得分如下:根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为
名选手的得分如下:根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为![]() 分),现得知
分),现得知![]() 号选手的综合成绩为
号选手的综合成绩为![]() 分.
分.
序号 |
|
|
|
笔试成绩/分 |
|
|
|
面试成绩/分 |
|
|
|
(1)求笔试成绩和面试成绩各占的百分比:
(2)求出其余两名选手的综合成绩,并以综合成绩排序确定这三名选手的名次。
查看答案和解析>>
科目:初中数学 来源: 题型:
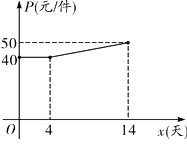
【题目】我市某企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:
![]()
(1)工人甲第几天生产的产品数量为70件?
(2)设第x天生产的产品成本为P元/件,P与![]() 的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班全体学生2018年初中毕业体育学业考试成绩统计表如下:
成绩/分 | 45 | 49 | 52 | 54 | 55 | 58 | 60 |
人数 | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
根据上表中信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是55分
C.该班学生这次考试成绩的中位数是55分
D.该班学生这次考试成绩的平均数是55分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校进行校园美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,如果由甲队先做20天,剩下的工程由甲、乙合作24天完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需要支付工程款3.5万元,乙队施工一天需要支付工程款2万元:如果规定在70天内完成这项工作,是由甲、乙两队单独完成省钱?还是由甲乙合作完成该工程省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com