
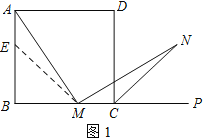
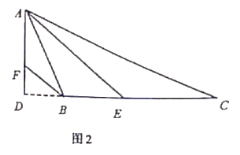
����Ŀ����1����ͼ1����������ABCD�У�M��BC�ߣ������˵�B��C��������һ�㣬P��BC�ӳ�����һ�㣬N�ǡ�DCP��ƽ������һ�㣮����AMN��90������֤��AM��MN��
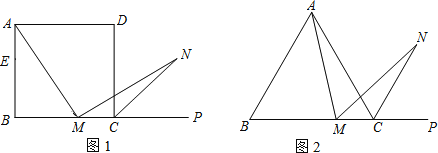
�������һ��֤����˼·���������һ˼·֤����Ҳ����ѡ������ķ���֤����
֤�����ڱ�AB�Ͻ�ȡAE��MC������ME��������ABCD�У���B����BCD��90����AB��BC�����NMC��180������AMN����AMB��180������B����AMB����MAB����MAE��
����������������µ�֤�����̣�
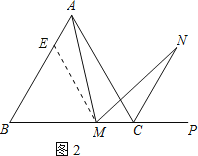
��2��������1���е���������ABCD����Ϊ����������ABC������ͼ2����N�ǡ�ACP��ƽ������һ�㣬���AMN��60��ʱ������AM��MN�Ƿ�������˵�����ɣ�
���𰸡���1������������2������AM��MN��������֤����������
��������
��1���ڱ�AB�Ͻ�ȡAE��MC������ME�������������ɵá�AEM=��MCN=135�����������Ǽ�һ�����ж�������ȫ�ȣ�
��2�������������Ǽ�һ��֤����ȫ�ȣ�֤������ͬ��1����
��1��֤�����ڱ�AB�Ͻ�ȡAE��MC������ME��
��������ABCD����B����BCD��90����AB��BC��
���NMC��180������AMN����AMB��180������B����AMB����MAB����MAE��
BE��AB��AE��BC��MC��BM��
���BEM��45�������AEM��135����
��N�ǡ�DCP��ƽ������һ�㣬
���NCP��45�������MCN��135����
����AEM����MCN����MAE����NMC��AE��MC����AEM����MCN��
���AEM�ա�MCN��ASA����
��AM��MN��
��2���⣺����AM��MN������
֤�����ڱ�AB�Ͻ�ȡAE��MC������ME��
������ABC����B����BCA��60����AB��BC��
���NMC��180������AMN����AMB��180������B����AMB����MAE��
BE��AB��AE��BC��MC��BM��
���BEM��60�������AEM��120����
��N�ǡ�ACP��ƽ������һ�㣬
���ACN��60�������MCN��120����
�ڡ�AEM���MCN�У���MAE����NMC��AE��MC����AEM����MCN��
���AEM�ա�MCN��ASA����
��AM��MN��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ϵ�����A��B��C�ֱ��ʾ������a��b��c����|a|��|c|��|b|��
��1������|a+c|��2|c��b|��
��2����b�ĵ���������������AB��BO��OC��6��2��3����1���д���ʽ��ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǹ�˾������ij��ʱ����Ʒÿ���ɱ�Ϊ20Ԫ�������г����з��֣�������Ʒ��δ��40���ڵ� ��������(��)��ʱ��(��)�Ĺ�ϵ���±���
ʱ��(��) | 1 | 3 | 6 | 10 | 36 | �� |
��������(��) | 94 | 90 | 84 | 76 | 24 | �� |
δ��40���ڣ�ǰ20��ÿ��ļ۸�y1(Ԫ/��)��tʱ��(��)�ĺ�����ϵʽΪ��y1=![]() t+25(1��t��20��tΪ����)����20��ÿ��ļ۸�y2(ԭ/��)��tʱ��(��)�ĺ�����ϵʽΪ��y2=��
t+25(1��t��20��tΪ����)����20��ÿ��ļ۸�y2(ԭ/��)��tʱ��(��)�ĺ�����ϵʽΪ��y2=��![]() t+40(21��t��40��tΪ����).�����������о� ������Ʒ���й�����.
t+40(21��t��40��tΪ����).�����������о� ������Ʒ���й�����.
(1)��������ϱ��е�������ϵ������ѧ����һ�κ��������κ��� ��������������֪ʶȷ��һ��������Щ����֮��ĺ�����ϵʽ��
(2)��Ԥ��δ��40������һ����������������������������Ƕ��٣�
(3)��ʵ�����۵�ǰ20���иù�˾����ÿ����һ����Ʒ�;���aԪ����(a��4)��ϣ�����̣���˾ͨ�����ۼ�¼���֣�ǰ20���У�ÿ��۳��������������������ʱ��t�������������a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���߹���ͼ����ͼ1�����ı���ABCD����һ��P��ʹ�õ�P��AB��BC�ľ�����ȣ����ҵ�P����A��D�ľ���Ҳ��ȣ�����д������������ͼ�ۼ�����
��2����ͼ2���ڳ���Ϊ1����λ���ȵ�С��������ɵ������������У���A��B��C��С�����εĶ����ϣ�����ABC�����Ϊ______��
����ͼ�л�������ABC����ֱ��l����ԳƵ���A1B1C1��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ӳ���Ͷ��һ�����͵��Ӳ�Ʒ��ÿ������ɱ�Ϊ18Ԫ�����������з��֣�ÿ��������![]() ������������۵���
������������۵���![]() ��Ԫ��֮��Ĺ�ϵ���Խ��Ƶؿ���һ�κ���
��Ԫ��֮��Ĺ�ϵ���Խ��Ƶؿ���һ�κ���![]() ��������=�ۼ�-����ɱ���
��������=�ۼ�-����ɱ���
��1��д��ÿ�µ�����![]() ����Ԫ�������۵���
����Ԫ�������۵���![]() ��Ԫ��֮��ĺ�����ϵʽ��
��Ԫ��֮��ĺ�����ϵʽ��
��2�������۵���Ϊ����Ԫʱ������ÿ�»�õ�����Ϊ440��Ԫ��
��3��������ز��Ź涨�����ֵ��Ӳ�Ʒ�����۵��۲��ܸ���40Ԫ���������ÿ�µ�����ɱ�������540��Ԫ����ô�����۵���Ϊ����Ԫʱ������ÿ�»�õ���������������Ϊ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:![]() ��,
��,![]() ��
��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�![]() ��
��![]() ��
��![]() ���ϵĸߣ�����
���ϵĸߣ�����![]() ��
��![]() ,��ֱ��
,��ֱ��![]() �ڵ�
�ڵ�![]() ��
��
![]() ��ͼ1,��
��ͼ1,��![]() ,��
,��![]() ___ ____;
___ ____;
![]() ��
��![]() �е�
�е�![]() ,��
,��![]() __ ____;(��
__ ____;(��![]() ��ʾ)
��ʾ)
![]() ��ͼ2,
��ͼ2,![]() �еĽ��ۻ�������?������,˵������;���������������
�еĽ��ۻ�������?������,˵������;���������������![]() ��(��
��(��![]() ��ʾ)
��ʾ)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�EΪBC����һ�㣬����AE����AE�Ĵ�ֱƽ���߽�AB��G����CD��F����DF��2��BG��4����GF�ij�Ϊ___________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
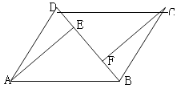
����Ŀ����![]() �У�BD������һ���Խ��ߣ���A��C����ֱ���
�У�BD������һ���Խ��ߣ���A��C����ֱ���![]() ��
��![]() ��E��FΪ���㣮
��E��FΪ���㣮
��1����ͼ����֤��![]() ��
��
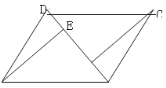
��2����ͼ������AC����AC��BD���ڵ�O����![]() ���ڲ������κθ����ߵ�����£���ֱ��д��ͼ�е����г�����OE����2�����߶Σ�
���ڲ������κθ����ߵ�����£���ֱ��д��ͼ�е����г�����OE����2�����߶Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ��ƸԱ������ȡ�������������ϵķ�ʽ���У�����ɼ���ԭʼ�־�Ϊ![]() ��.ǰ
��.ǰ![]() ��ѡ�ֵĵ÷����£����ݹ涨�����Գɼ������Գɼ��ֱ�һ���İٷֱ��ۺϳ��ۺϳɼ����ۺϳɼ���������Ϊ
��ѡ�ֵĵ÷����£����ݹ涨�����Գɼ������Գɼ��ֱ�һ���İٷֱ��ۺϳ��ۺϳɼ����ۺϳɼ���������Ϊ![]() �֣����ֵ�֪
�֣����ֵ�֪![]() ��ѡ�ֵ��ۺϳɼ�Ϊ
��ѡ�ֵ��ۺϳɼ�Ϊ![]() ��.
��.
��� |
|
|
|
���Գɼ�/�� |
|
|
|
���Գɼ�/�� |
|
|
|
��1������Գɼ������Գɼ���ռ�İٷֱȣ�
��2�������������ѡ�ֵ��ۺϳɼ��������ۺϳɼ�����ȷ��������ѡ�ֵ����Ρ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com