
【题目】如图,数轴上的三点A、B、C分别表示有理数a、b、c,且|a|>|c|>|b|.
(1)化简|a+c|﹣2|c﹣b|;
(2)若b的倒数是它本身,且AB:BO:OC=6:2:3,求(1)中代数式的值.
![]()
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系![]() 中,正比例函数
中,正比例函数![]() 与一次函数
与一次函数![]() 的图象相交于点
的图象相交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,分别交正比例函数的图像于点B,交一次函数的图象于点C,连接OC.
轴的垂线,分别交正比例函数的图像于点B,交一次函数的图象于点C,连接OC.
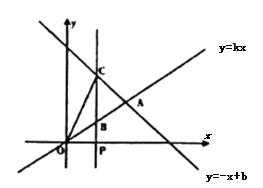
(1)求这两个函数解析式.
(2)求![]() 的面积.
的面积.
(3)在坐标轴上存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形,请直接写出
为腰的等腰三角形,请直接写出![]() 点的坐标。
点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公司有三个住宅区,A、B、C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
![]()
A. 点AB. 点BC. A,B之间D. B,C之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P(m,n)是抛物线y=![]() -1上任意一点,l是过点(0,-2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
-1上任意一点,l是过点(0,-2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
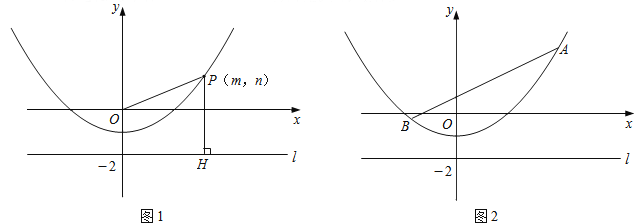
【探究】
(1)填空:当m=0时,OP= ,PH= ;当m=4时,OP= ,PH= ;
【证明】
(2)对任意m,n,猜想OP与PH的大小关系,并证明你的猜想.
【应用】
(3)如图2,已知线段AB=6,端点A,B在抛物线y=![]() -1上滑动,求A,B两点到直线l的距离之和的最小值.
-1上滑动,求A,B两点到直线l的距离之和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
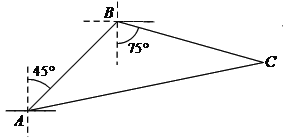
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
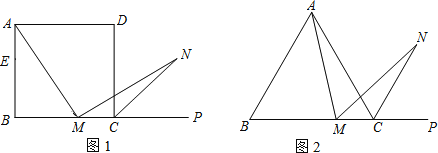
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com