
����Ŀ����ͼ1��P��m��n����������y=![]() -1������һ�㣬l�ǹ�����0��-2������x��ƽ�е�ֱ�ߣ�����P��ֱ��PH��l������ΪH��
-1������һ�㣬l�ǹ�����0��-2������x��ƽ�е�ֱ�ߣ�����P��ֱ��PH��l������ΪH��
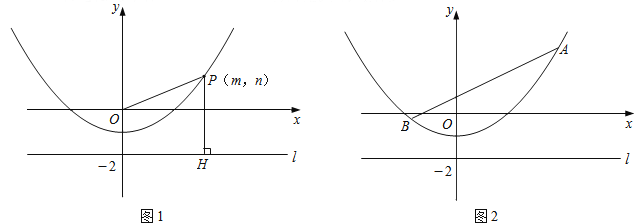
��̽����
��1����գ���m=0ʱ��OP= ��PH= ����m=4ʱ��OP= ��PH= ��
��֤����
��2��������m��n������OP��PH�Ĵ�С��ϵ����֤����IJ�����
��Ӧ�á�
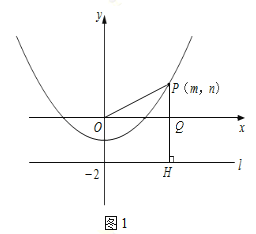
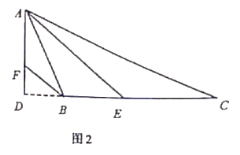
��3����ͼ2����֪�߶�AB=6���˵�A��B��������y=![]() -1�ϻ�������A��B���㵽ֱ��l�ľ���֮�͵���Сֵ��
-1�ϻ�������A��B���㵽ֱ��l�ľ���֮�͵���Сֵ��
���𰸡���1��OP=1��PH=1��OP=5��PH=5����2��OP=PH��֤������������3��6��
��������
������1��m��ΪP��ĺ�������m=0ʱ��ֱ�Ӵ���x=0����P��0��-1������OP��PH����֪����m=4ʱ��ֱ�Ӵ���x=4����P��4��3����OP���й��ɶ�����ã�PH=yP-��-2����
��2������OP=PH��֤��ʱ��ΪPΪ����������κ���y=![]() -1�ĵ㣬һ�������m��
-1�ĵ㣬һ�������m��![]() -1����������1�����ù��ɶ�����PH=yP-��-2�������OP��PH���Ƚϼ��ý�����
-1����������1�����ù��ɶ�����PH=yP-��-2�������OP��PH���Ƚϼ��ý�����
��3��������2�����ۣ�������y=![]() -1�ĵ㵽ԭ��ľ�������䵽l�ľ�����Ҫ��A��B���㵽l����ĺͣ���A��B���㵽ԭ��ĺͣ���AB������O����OA+OB��AB=6����AB����O����OA+OB=AB=6������OA+OB��6����A��B���㵽l����ĺ͡�6��������Сֵ��Ϊ6��
-1�ĵ㵽ԭ��ľ�������䵽l�ľ�����Ҫ��A��B���㵽l����ĺͣ���A��B���㵽ԭ��ĺͣ���AB������O����OA+OB��AB=6����AB����O����OA+OB=AB=6������OA+OB��6����A��B���㵽l����ĺ͡�6��������Сֵ��Ϊ6��
�����������1���⣺OP=1��PH=1��OP=5��PH=5��
��ͼ1����PH��x�ύ��ΪQ��
��m=0ʱ��P��0��-1������ʱOP=1��PH=1��
��m=4ʱ��P��4��3������ʱPQ=3��OQ=4��
��OP=![]() =5��PH=yP-��-2��=3-��-2��=5��
=5��PH=yP-��-2��=3-��-2��=5��
��2�����룺OP=PH��
֤��������P��PQ��x����Q��
��P�ڶ��κ���y=![]() -1�ϣ�
-1�ϣ�
����P��m��![]() -1������PQ=|
-1������PQ=|![]() -1|��OQ=|m|��
-1|��OQ=|m|��
�ߡ�OPQΪֱ�������Σ�
��OP=![]() ��
��
PH=yP-��-2��=��![]() -1��-��-2��=
-1��-��-2��=![]() ��
��
��OP=PH��
��3���⣺��ͼ2������OA��OB������A��AC��l��C������B��BD��l��D����ʱAC��ΪA�㵽l�ľ��룬BD��ΪB�㵽l�ľ�����
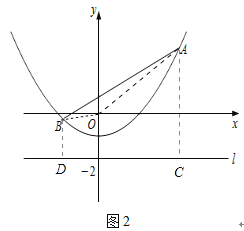
����AB����O��ʱ������OA��OB��
����OAB��OA+OB��AB=6��
���������۵ã�AC=OA��BD=OB��
��AC+BD��6��
����AB��O��ʱ��AC+BD=OA+OB=AB=6��
����AC+BD����СֵΪ6��
��A��B���㵽ֱ��l�ľ���֮�͵���СֵΪ6��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() �У�
��![]() ��
��![]() ����
����![]() �Ƶ�
�Ƶ�![]() ˳ʱ�뷽����ת
˳ʱ�뷽����ת![]() ��
��![]() ��λ�ã�����
��λ�ã�����![]() ����
����![]() �ij�Ϊ( )
�ij�Ϊ( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��һ�����Ӷ����Ժ����߶�![]() ��ʾ,�ִ�
��ʾ,�ִ�![]() �������Ӽ���,���Ϻ�ĸ������������һ��Ϊ
�������Ӽ���,���Ϻ�ĸ������������һ��Ϊ![]() ����
����![]() �����������ӵ�ԭ��Ϊ�� ��
�����������ӵ�ԭ��Ϊ�� ��
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(��������8��) 2011��5����Ѯ������������35000����ѧ���μ��п��������ԣ�Ϊ���˽���꼶����������Զ�ijɼ�����ijУ�����ȡ��50�������IJ��Գɼ�����
�ݲ������ֱ��������ǵĵ÷ְ����㡢���á��������ֱ���A��B��C��D
��ʾ���ĸ��ȼ�����ͳ�ƣ������Ƴ���ͼ��ʾ������ͼ��ͳ�Ʊ���
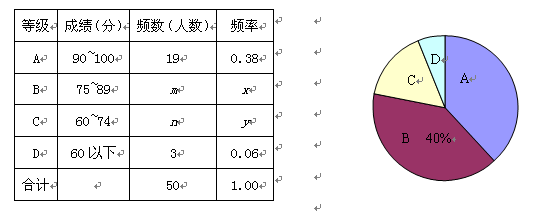
�����������ͼ���ṩ����Ϣ������������⣺
��1��(1) m�� ��n�� ��x�� ��y�� ��
��2��(2)������ͼ�У�C�ȼ�����Ӧ��Բ�Ľ��� �ȣ�
��3��(3)�����У���꼶����500�������μ���������Զ���ԣ���ô���������Щ�����ɼ��ȼ��ﵽ��������õĹ��ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ϵ�����A��B��C�ֱ��ʾ������a��b��c����|a|��|c|��|b|��
��1������|a+c|��2|c��b|��
��2����b�ĵ���������������AB��BO��OC��6��2��3����1���д���ʽ��ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ֱ���![]() �ı�������������ABFG��ACDE������EG����OΪEG���е㣬
�ı�������������ABFG��ACDE������EG����OΪEG���е㣬
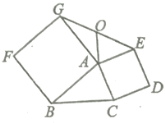
��֤����1��![]() ��
��
��2��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��̨������λ�ڵ�P�����ض�������PQ�ƶ�����̨֪���ƶ����ٶ�Ϊ30 km/h����Ӱ������İ뾶Ϊ200 km��B��λ�ڵ�P�ı�ƫ��75���������������P 320 km��������̨���Ƿ��Ӱ��B�У���Ӱ����������̨��Ӱ��B�е�ʱ�䣻����Ӱ������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��������ʯ�ӿ��ڳ���ͼ��ʾ�������κ��ı��Σ���ϣ����ѧ�Ұ���1,3,6,10,15,21��...��Ϊ����������������1,4,9,25��...��Ϊ������������.ͬ������1,5,12,22��...��������Ϊ�����������.
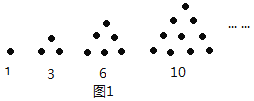
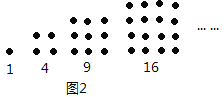
�������Ρ������Ρ�����ζ������������������ʾ�����

��1�����չ��ɣ�������a=_______________��b=_________________��c=________________________
��2���۲���й��ɣ���n����������������_________________������n����������������x�����ú�x��n�Ĵ���ʽ��ʾ��n��������������� ______________________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:![]() ��,
��,![]() ��
��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�![]() ��
��![]() ��
��![]() ���ϵĸߣ�����
���ϵĸߣ�����![]() ��
��![]() ,��ֱ��
,��ֱ��![]() �ڵ�
�ڵ�![]() ��
��
![]() ��ͼ1,��
��ͼ1,��![]() ,��
,��![]() ___ ____;
___ ____;
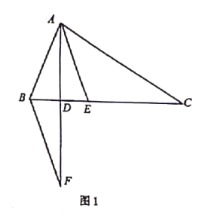
![]() ��
��![]() �е�
�е�![]() ,��
,��![]() __ ____;(��
__ ____;(��![]() ��ʾ)
��ʾ)
![]() ��ͼ2,
��ͼ2,![]() �еĽ��ۻ�������?������,˵������;���������������
�еĽ��ۻ�������?������,˵������;���������������![]() ��(��
��(��![]() ��ʾ)
��ʾ)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com