
【题目】如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30 km/h,受影响区域的半径为200 km,B市位于点P的北偏东75°方向上,距离点P 320 km处.本次台风是否会影响B市?若影响,求出这次台风影响B市的时间;若不影响,请说明理由.

【答案】有影响;8h.
【解析】作BH⊥PQ于点H,在Rt△BHP中,利用特殊角的三角函数值求出BH的长与200千米相比较即可;以B为圆心,以200为半径作圆交PQ于P1、P2两点,根据垂径定理即可求出P1P2的长,进而求出台风影响B市的时间.
如答图,作BH⊥PQ于点H.
∵在Rt△BHP中,PB=320 km,∠BPQ=30°,
∴BH=320×sin30°=160(km).
∵160 km<200 km,
∴本次台风会影响B市;
如答图,设台风中心移动到P1时,台风开始影响B市,台风中心移动到P2时,台风影响结束.
∵BH=160 km,BP1=BP2=200 km,
∴P1P2=2![]() =240(km),
=240(km),
∴台风影响B市的时间t=![]() =8(h).
=8(h).
答:这次台风影响B市8 h.



科目:初中数学 来源: 题型:
【题目】如图1,P(m,n)是抛物线y=![]() -1上任意一点,l是过点(0,-2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
-1上任意一点,l是过点(0,-2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
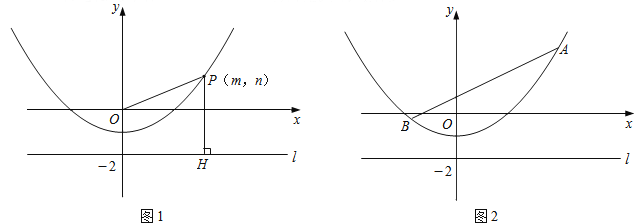
【探究】
(1)填空:当m=0时,OP= ,PH= ;当m=4时,OP= ,PH= ;
【证明】
(2)对任意m,n,猜想OP与PH的大小关系,并证明你的猜想.
【应用】
(3)如图2,已知线段AB=6,端点A,B在抛物线y=![]() -1上滑动,求A,B两点到直线l的距离之和的最小值.
-1上滑动,求A,B两点到直线l的距离之和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
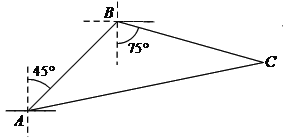
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为斜边AB的中点,动点P从B出发,沿B→C→A运动,如图(1)所示,设S△DPB=y,点P运动的路程为x,若y与x之间的函数关系图象如图(2)所示,则图(2)中Q点的坐标是( )
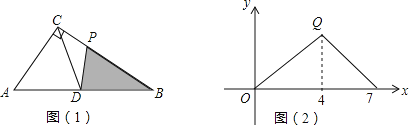
A. (4,2) B. (4,3) C. (4,4) D. (4,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6a,BC=6b,∠D=60°,点E、F、G、H分别在ABCD各边上,且BE=DG=![]() AE,CF=AH=
AE,CF=AH=![]() BF.
BF.
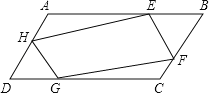
(1)求证:四边形EFGH是平行四边形;
(2)若四边形EFGH是菱形,求![]() 的值;
的值;
(3)四边形EFGH能为正方形吗?若能,请直接写出a、b的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:在图(1)(2)所示抛物线中,抛物线与![]() 轴交于
轴交于![]() 、
、![]() ,与
,与![]() 轴交于
轴交于![]() ,点
,点![]() 是抛物线的顶点,过
是抛物线的顶点,过![]() 平行于
平行于![]() 轴的直线是它的对称轴,点
轴的直线是它的对称轴,点![]() 在对称轴上运动。仅用无刻度的直尺画线的方法,按要求完成下列作图:
在对称轴上运动。仅用无刻度的直尺画线的方法,按要求完成下列作图:

(1)在图①中作出点![]() ,使线段
,使线段![]() 最小;
最小;
(2)在图②中作出点![]() ,使线段
,使线段![]() 最大.
最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com