
 ��֪���κ���y=��x-m��2+n��m��nΪ��������
��֪���κ���y=��x-m��2+n��m��nΪ������������ ��1���ٸ���ƽ�ƹ��ɵõ�m��n��ֵ���������߽���ʽ�����B��C�����ꣻ
�����ù��ɶ������涨������֤����
�۽�ϵ��������ε����ʡ�����������֪��PBO=��CBD��ͨ��������Ǻ����Ķ��������P�����ꣻ
��2����Ҫ��m��ȡֵ��Χ���з������ۣ���������ߵ�����������m��ֵ��
��� 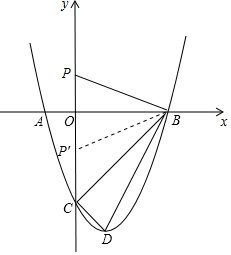 �⣺��1���ٶ��κ���y=x2��ͼ��������ƽ��1����λ���ȣ�������ƽ��4����λ���ȵõ������߽���ʽΪ��y=��x-1��2-4����m=1��n=-4��
�⣺��1���ٶ��κ���y=x2��ͼ��������ƽ��1����λ���ȣ�������ƽ��4����λ���ȵõ������߽���ʽΪ��y=��x-1��2-4����m=1��n=-4��
��x=0����y=3����C��0��-3����
��y=0����x-1��2-4=0����x=3��x=-1����Ϻ���ͼ��֪��B��3��0����
�ʴ��ǣ�1��-4����3��0������0��-3����
�ڡ�BCDΪֱ�������Σ�֤�����£�
�������߽���ʽΪ��y=��x-1��2-4�õ�D��1��-4����
��B��3��0����C��0��-3����
��CD2=��1-0��2+��-4+3��2=2��BC2=32+32=18��BD2=��1-3��2+��-4-0��2=20��
��CD2+BC2=BD2��
���BCDΪֱ�������Σ�
�ۡ�B��3��0����C��0��-3����
��OB=OC��
���OCB=��OBC��
�ߡ�PBO+��OCB=��OBD��
���PBO+��OBC=��OBC+��CBD��
���PBO=��CBD��
��tan��PBO=tan��CBD����$\frac{OP}{3}$=$\frac{\sqrt{2}}{3\sqrt{2}}$����OP=1����P��0����1����
��2����n=1-m2��
��y=��x-m��2+1-m2��
��Գ�����x=m��
�ٵ�m��-2ʱ��ȡx=-2ʱ��y��Сֵ=��-2-m��2+1-m2=-2��
���m=$-\frac{7}{4}$����ȥ��
�ڵ�-2��m��1ʱ��ȡx=mʱ��y��Сֵ=��m-m��2+1-m2=-2��
��ã�m1=$-\sqrt{3}$��m2=$\sqrt{3}$����ȥ����
�۵�m��1ʱ��ȡx=1ʱ��y��Сֵ=��1-m��2+1-m2=-2��
���m=2��
����������m��ֵ��-$\sqrt{3}$��2��
���� ������Ҫ�����˶��κ����Ľ���ʽ�����뼸��ͼ�ν�ϵ��ۺ�������������Ҫ���������ν�ϵ�˼��Ѵ����ͼ���ͼ�ν�����������õ������������ʾ�߶εij��ȣ��Ӷ�����߶�֮��Ĺ�ϵ��


 53������ϵ�д�
53������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ABC�У�D��E��AB��AC�ϵ㣬AB=7.8��AD=3��AC=6��AE=3.9�����жϡ�ADE���ABC�Ƿ�����ƣ�
��ͼ��ABC�У�D��E��AB��AC�ϵ㣬AB=7.8��AD=3��AC=6��AE=3.9�����жϡ�ADE���ABC�Ƿ�����ƣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��Rt��ABC�У���ACB=90�㣬AC=BC��DΪBC�е㣬��D����ֱ��
��Rt��ABC�У���ACB=90�㣬AC=BC��DΪBC�е㣬��D����ֱ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����֪OCƽ�֡�AOB��CD��OB����OD=4cm����CD���ڣ�������
��ͼ��ʾ����֪OCƽ�֡�AOB��CD��OB����OD=4cm����CD���ڣ�������| A�� | 1.5cm | B�� | 2cm | C�� | 3cm | D�� | 4cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 A��B�������600ǧ�ף��ס���������A�dz���ʻ��B�ǣ��ҳ����ٶ�Ϊ75ǧ��/ʱ���׳�����100ǧ���ҳ��ų������׳�����Bж�������������A�ǣ���ͼ������A�ǵľ���y��ǧ�ף����ҳ���ʻʱ��x��Сʱ��֮��ĺ���ͼ��
A��B�������600ǧ�ף��ס���������A�dz���ʻ��B�ǣ��ҳ����ٶ�Ϊ75ǧ��/ʱ���׳�����100ǧ���ҳ��ų������׳�����Bж�������������A�ǣ���ͼ������A�ǵľ���y��ǧ�ף����ҳ���ʻʱ��x��Сʱ��֮��ĺ���ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 289��1-2x��=256 | B�� | 256��1+x��2=289 | ||
| C�� | 289��1-x��2=256 | D�� | 289-289��1-x��-289��1-x��2=256 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com