
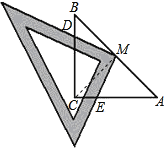
【题目】如图,已知:Rt△ABC中,∠C=90°,AC=BC=2,将一块三角尺的直角顶点与斜边AB的中点M重合,当三角尺绕着点M旋转时,两直角边始终保持分别与边BC、AC交于D,E两点(D、E不与B、A重合).
(1)求证:MD=ME;
(2)求四边形MDCE的面积;

【答案】(1)证明见解析(2)1
【解析】
(1)连接CM,根据∠BMD=90°﹣∠DMC,∠EMC=90°﹣∠DMC,可证明∠BMD=∠CME,根据等腰直角三角形的性质可得∠B=∠MCA=45°.根据直角三角形斜边中线的性质可得CM=BM,即可证明△BDM≌△CEM,然后即可证MD=ME;(2)利用三角形全等可知四边形MDCE的面积等于△CMB的面积,即可得答案.
(1)证明:连接CM,在Rt△ABC中,M是AB的中点,且AC=BC,
∴CM=AB=BM,
∠MCA=∠B=45°,CM⊥AB,
而∠BMD=90°﹣∠DMC,∠EMC=90°﹣∠DMC.
∴∠BMD=∠EMC.
△BDM≌△CEM(ASA).
∴MD=ME
(2)∵△BDM≌△CEM,
∴S四边形MDCE=S△DMC+S△CME=S△DMC+S△BMD=S△BCM=![]() S△ACB=
S△ACB=![]() ×
×![]() ×2×2=1.
×2×2=1.
∴四边形MDCE的面积为1;


科目:初中数学 来源: 题型:
【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查.下面是根据收集的数据绘制的两幅不完整的统计图.
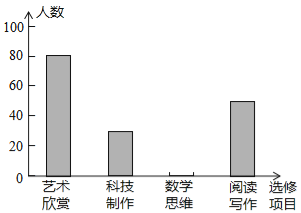
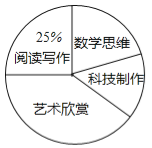
请根据图中提供的信息,解答下面的问题:
(1)此次共调查了 名学生,扇型统计图中“艺术鉴赏”部分的圆心角是 度.
(2)请把这个条形统计图补充完整.
(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修“科技制作”项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距50km,甲于某日骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,在这个变化过程中,甲和乙所行驶的路程用变量s(km)表示,甲所用的时间用变量t(时)表示,图中折线OPQ和线段MN分别表示甲和乙所行驶的路程s与时间t的变化关系,请根据图象回答:

(1)直接写出:甲出发后______小时,乙才开始出发;
(2)请分别求出甲出发1小时后的速度和乙的行驶速度?
(3)求乙行驶几小时后追上甲,此时两人距B地还有多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠MON=90°,点A,B分别在OM、ON上运动(不与点O重合).
(1)如图①,AE、BE分别是∠BAO和∠ABO的平分线,随着点A、点B的运动,∠AEB= °
(2)如图②,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D
①若∠BAO=60°,则∠D= °.
②随着点A,B的运动,∠D的大小会变吗?如果不会,求∠D的度数;如果会,请说明理由.
(3)如图③,延长MO至Q,延长BA至G,已知∠BAO,∠OAG的平分线与∠BOQ的平分线及其延长线相交于点E、F,在△![]() 中,如果有一个角是另一个角的3倍,求∠ABO的度数.
中,如果有一个角是另一个角的3倍,求∠ABO的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(3,0),顶点B在y轴正半轴上,顶点D在x轴负半轴上.若抛物线y=﹣x2﹣5x+c经过点B、C,则菱形ABCD的面积为 . 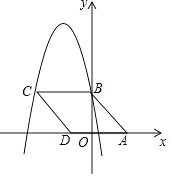
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.若AC=4,则EG2+FH2=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=![]() x与直线l2交点A的横坐标为2,将直线l1沿y轴向下平移4个单位长度,得到直线l3,直线l3与y轴交于点B,与直线l2交于点C,点C的纵坐标为-2.直线l2与y轴交于点D.
x与直线l2交点A的横坐标为2,将直线l1沿y轴向下平移4个单位长度,得到直线l3,直线l3与y轴交于点B,与直线l2交于点C,点C的纵坐标为-2.直线l2与y轴交于点D.
(1)求直线l2的解析式;
(2)求△BDC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com