
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(3,0),顶点B在y轴正半轴上,顶点D在x轴负半轴上.若抛物线y=﹣x2﹣5x+c经过点B、C,则菱形ABCD的面积为 . 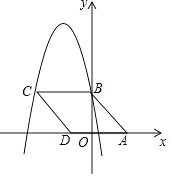
科目:初中数学 来源: 题型:
【题目】在如下命题中:(1)过一点有且只有一条直线与已知直线垂直;(2)垂线段最短;(3)过一点有且只有一条直线与这条直线平行;(4)内错角相等;(5)平行于同一直线的两直线平行;(6)有两个角互余的三角形是直角三角形是真命题的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 为平面内一点.
为平面内一点.
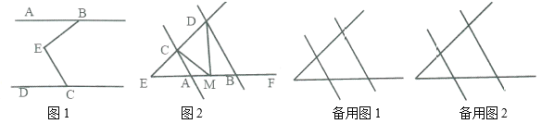
(1)如图1,![]() 和
和![]() 互余,小明说过
互余,小明说过![]() 作
作![]() ,很容易说明
,很容易说明![]() 。请帮小明写出具体过程;
。请帮小明写出具体过程;
(2)如图2,![]() ,当点
,当点![]() 在线段
在线段![]() 上移动时(点
上移动时(点![]() 与
与![]() ,
,![]() 两点不重合),指出
两点不重合),指出![]() 与
与![]() ,
,![]() 的数量关系?请说明理由;
的数量关系?请说明理由;
(3)在(2)的条件下,若点![]() 在
在![]() ,
,![]() 两点外侧运动(点
两点外侧运动(点![]() 与
与![]() ,
,![]() ,
,![]() 三点不重合)请直接写出
三点不重合)请直接写出![]() 与
与![]() ,
,![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
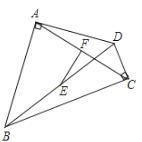
【题目】如图,四边形ABCD中,∠BAD=90°,∠DCB=90°,EF分别是BD、AC的中点,
(1)请你猜测EF与AC的位置关系,并给予证明;
(2)当AC=8,BD=10时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:Rt△ABC中,∠C=90°,AC=BC=2,将一块三角尺的直角顶点与斜边AB的中点M重合,当三角尺绕着点M旋转时,两直角边始终保持分别与边BC、AC交于D,E两点(D、E不与B、A重合).
(1)求证:MD=ME;
(2)求四边形MDCE的面积;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3个完全相同的小球,把它们分别标号为1,2,3,放在一个不透明的口袋中,从口袋中随机摸出一个小球,记下标号后放回,再从口袋中随机摸出一个小球,记下标号.用画树状图(或列表)的方法,求两次摸出的小球号码恰好都大于1的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
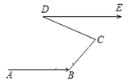
【题目】“浏阳河弯过九道弯,五十里水路到湘江.”如图所示,某段河水流经 B,C,D 三点拐弯后与原来流向相同,若∠ABC =6∠CDE,∠BCD =4∠CDE,则∠CDE= _________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD的纸片中,AC⊥AB,AC与BD交于O,将△ABC沿对角线AC翻折得到![]() .
.
(1)求证:四边形ACDB’是矩形.
(2)若平行四边形ABCD的面积为12,求翻折后纸片重叠部分的面积,即![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖为妈妈准备了一份生日礼物,礼物外包装盒为长方体形状,长、宽、高分别为![]() 、
、![]() 、
、![]()
![]() ,为了美观,小颖决定在包装盒外用丝带打包装饰,她发现,可以用如图所示的三种打包方式,所需丝带的长度分别为
,为了美观,小颖决定在包装盒外用丝带打包装饰,她发现,可以用如图所示的三种打包方式,所需丝带的长度分别为![]() ,
,![]() ,
,![]() (不计打结处丝带长度)
(不计打结处丝带长度)

(1)用含![]() 、
、![]() 、
、![]() 的代数式分别表示
的代数式分别表示![]() ,
,![]() ,
,![]() ;
;
(2)方法简介:
要比较两数![]() 与
与![]() 大小,我们可以将
大小,我们可以将![]() 与
与![]() 作差,结果可能出现三种情况:
作差,结果可能出现三种情况:
①![]() ,则
,则![]() ;
;
②![]() ,则
,则![]() ;
;
③![]() ,则
,则![]() ;
;
我们将这种比较大小的方法叫做“作差法”.
请帮小颖选出最节省丝带的打包方式,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com