Question

20．在Rt△ABC纸片中，∠ACB=90°，AC=6，BC=8，P是AB边上一点，连接CP．沿CP把Rt△ABC纸片裁开，要使△ACP是等腰三角形，那么AP的长度是6，5或$\frac{36}{5}$．

Answer 1

分析 此题要分三种情况进行讨论：AP″=AC=6时，△ACP″是等腰三角形；CP=AP时，△ACP是等腰三角形；CP′=AC时，△ACP′是等腰三角形，分别计算出AP的长度．

解答 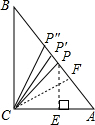解：①如图：AP″=AC=6时，△ACP″是等腰三角形；
②CP=AP时，△ACP是等腰三角形；
过P作PE⊥AC，
∵CP=AP，
∴AE=$\frac{1}{2}$AC=3，
∵∠ACB=90°，
∴PE∥CB，
∴PE=$\frac{1}{2}$CB=4，
∴AP=$\sqrt{{4}^{2}+{3}^{2}}$=5；
③CP′=AC时，△ACP′是等腰三角形，
过C作CF⊥AB，
∴AP′=2AF，
∵AC=6，
∴CP′=6，
∵∠ACB=90°，AC=6，BC=8，
∴AB=10，
∴cosA=$\frac{BC}{AB}$=$\frac{3}{5}$，
∴$\frac{AF}{AC}$=$\frac{3}{5}$，
∴AF=$\frac{3}{5}$×6=$\frac{18}{5}$，
∴AP′=$\frac{36}{5}$，
故答案为：6，5或$\frac{36}{5}$．

点评 此题主要考查了三角形中位线定理、勾股定理的应用，以及等腰三角形的性质，关键是掌握等腰三角形三线合一．