
【题目】计算:
(1)(a+b)2﹣b(2a+b)
(2)( ![]() +x﹣1)÷
+x﹣1)÷ ![]() .
.
【答案】
(1)
解(a+b)2﹣b(2a+b)
=a2+2ab+b2﹣2ab﹣b2
=a2;
(2)
解:( ![]() +x﹣1)÷
+x﹣1)÷ ![]()
= ![]() ×
× ![]()
= ![]() ×
× ![]()
= ![]() .
.
【解析】(1)根据完全平方公式和单项式乘多项式的法则计算即可;(2)根据分式的混合运算法则进行计算.本题考查的是整式的混合运算、分式的混合运算,掌握完全平方公式、分式的混合运算法则是解题的关键.
【考点精析】关于本题考查的分式的混合运算,需要了解运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]}才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF
(2)若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,E为矩形ABCD边AD上的一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是2cm/s.若P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t的函数关系图象如图2,则下列结论错误的是( )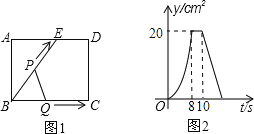
A.AE=12cm
B.sin∠EBC=![]()
C.当0<t≤8时,y=![]() t2
t2
D.当t=9s时,△PBQ是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组建了书法、音乐、美术、舞蹈、演讲五个社团,全校1600名学生每人都参加且只参加了其中一个社团的活动.校团委从这1600名学生中随机选取部分学生进行了参加活动情况的调查,并将调查结果制成了如图不完整的统计图.请根据统计图完成下列问题: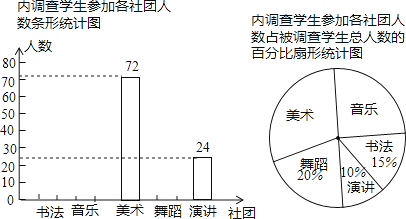
参加本次调查有名学生,根据调查数据分析,全校约有名学生参加了音乐社团;请你补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )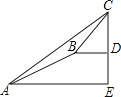
A.8.1米
B.17.2米
C.19.7米
D.25.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣ ![]() x2+
x2+ ![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.
(1)判断△ABC的形状,并说明理由;
(2)经过B,C两点的直线交抛物线的对称轴于点D,点P为直线BC上方抛物线上的一动点,当△PCD的面积最大时,Q从点P出发,先沿适当的路径运动到抛物线的对称轴上点M处,再沿垂直于抛物线对称轴的方向运动到y轴上的点N处,最后沿适当的路径运动到点A处停止.当点Q的运动路径最短时,求点N的坐标及点Q经过的最短路径的长;
(3)如图2,平移抛物线,使抛物线的顶点E在射线AE上移动,点E平移后的对应点为点E′,点A的对应点为点A′,将△AOC绕点O顺时针旋转至△A1OC1的位置,点A,C的对应点分别为点A1 , C1 , 且点A1恰好落在AC上,连接C1A′,C1E′,△A′C1E′是否能为等腰三角形?若能,请求出所有符合条件的点E′的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护视力要求人写字时眼睛和笔端的距离应超过30cm,图1是一位同学的坐姿,把他的眼睛B,肘关节C和笔端A的位置关系抽象成图2的△ABC,已知BC=30cm,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
A.30°
B.45°
C.60°
D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 40 | 60 | 100 |
根据图表提供的信息,下列结论错误的是( )
A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E,F的人数分别为80,70
D.喜欢选修课C的人数最少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com