
【题目】(9分)已知如图(1):△ABC中,AB=AC,∠B、∠C的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.

(1)写出线段EF与BE、CF间的数量关系?(不证明)
(2)若AB≠AC,其他条件不变,如图(2),图中线段EF与BE、CF间是否存在(1)中数量关系?请说明理由.
(3)若△ABC中,AB≠AC,∠B的平分线与三角形外角∠ACD的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F,如图(3),这时图中线段EF与BE,CF间存在什么数量关系?请说明理由.
【答案】(1)EF=BE+CF;(2)仍然有EF=BE+CF,理由见解析;(3)EF=BE﹣CF,理由见解析.
【解析】
试题(1)根据角平分线的定义可得∠EBO=∠OBC,已知EF∥BC,根据平行线的性质可得∠EOB=∠OBC,所以∠EOB=∠EBO,再由等腰三角形的判定可得OE=BE.同理可得OF=FC,所以EF=EO+OF=BE+CF;(2)仍然存在EF=BE+CF,根据(1)的方法即可证得结论;
(3)EF=BE﹣CF,利用(1)的方法可证得EO=BE,FO=CF,可得到EF=BE﹣CF.
试题解析:解:(1)EF=BE+CF;
(2)仍然有EF=BE+CF.理由如下:
∵EF∥BC,
∴∠EOB=∠OBC,
∵BO平分∠ABC,
∴∠EBO=∠OBC,
∴∠EOB=∠EBO,
∴OE=BE,同理OF=FC,
∴EF=EO+OF=BE+CF;
(3)EF=BE﹣CF.理由如下:
∵OE∥BC,
∴∠EOC=∠OCD,
∵CO平分∠ACD,
∴∠FCO=∠OCD,
∴∠FCO=∠FOC,
∴OF=CF,
同理可得到BE=EO,
∴EF=EO﹣FO=BE﹣CF.


科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
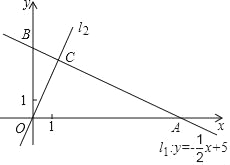
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论: ①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )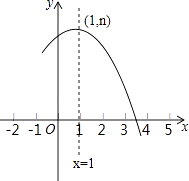
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑工程队利用一面墙(墙的长度不限),用40米长的篱笆围成一个长方形的仓库. 
(1)求长方形的面积是150平方米,求出长方形两邻边的长;
(2)能否围成面积220平方米的长方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店老板去批发市场购买某种图书.第一次用1200元购书若干本,并按该书定价20元出售,很快售完.由于该书畅销,第二次购书时,每本书批发价比第一次提高了25%,他用1800元所购该书数量比第一次多20本,又按定价售出全部图书.
(1)求该书原来每本的批发价;
(2)该老板这两次售书一共赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5
B.6
C.7
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com