
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 先根据勾股定理的逆定理对①②④⑤中△ABC的形状进行判断;再根据三角形的内角和是180°对③中△ABC的形状作出判断即可.
解答 解:①∵($\frac{1}{5}$)2+($\frac{1}{4}$)2≠($\frac{1}{3}$)2,
∴c2+b2≠a2,
∴△ABC不是直角三角形;
②∵52+122=132,
∴a2+b2=c2,
∴△ABC是直角三角形;
③∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,
∴∠C=90°,△ABC是直角三角形;
④∵92+402=412,
∴a2+b2=c2,
∴△ABC是直角三角形;
⑤∵32+32≠42,
∴a2+b2≠c2,
∴△ABC不是直角三角形;
其中是直角三角形的是②③④,有3个,
故选:B
点评 本题考查勾股定理的逆定理、三角形内角和定理.判断三角形是否为直角三角形,可利用勾股定理的逆定理和直角三角形的定义判断.


科目:初中数学 来源: 题型:填空题
 如图,小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会(只填序号)①.①越来越长,②越来越短,③长度不变.
如图,小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会(只填序号)①.①越来越长,②越来越短,③长度不变.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
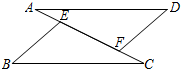 如图所示,已知AE=CF,∠A=∠C,要使△BCE≌△DAF,还需添加一个条件(只需填一个即可)AD=BC或∠B=∠D或∠CEB=∠AFD.
如图所示,已知AE=CF,∠A=∠C,要使△BCE≌△DAF,还需添加一个条件(只需填一个即可)AD=BC或∠B=∠D或∠CEB=∠AFD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com