
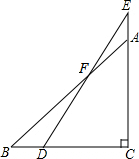
 在△ABC中,∠C=90°,∠B=55°点D在边BC上,点E在CN的延长线上,连接DE,∠E=25°,求∠BFD的度数.
在△ABC中,∠C=90°,∠B=55°点D在边BC上,点E在CN的延长线上,连接DE,∠E=25°,求∠BFD的度数. 科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:填空题
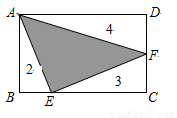
如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,
则△AEF的面积为______.
查看答案和解析>>
科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:单选题
在-2、0、1、2这四个数中,最小的数是( )
A. -2 B. 0 C. 1 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
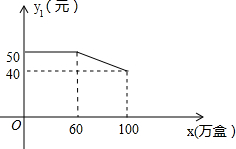 有一个茶叶厂,该厂的茶叶主要有两种销售方式,一种方式是卖给茶叶经销商,另一种方式是在各超市的柜台进行销售,每年该厂生产的茶叶都可以全部销售,该茶叶厂每年可以生产茶叶100万盒,其中,卖给茶叶经销商每盒茶叶的利润y1(元)与销售量x(万盒)之间的函数关系如图所示;在各超市柜台销售的每盒利润y2(元)与销售量x(万盒)之间的函数关系为:y2=$\left\{\begin{array}{l}{40(0≤x≤60)}\\{\frac{3}{4}x+5(60<x≤100)}\end{array}\right.$
有一个茶叶厂,该厂的茶叶主要有两种销售方式,一种方式是卖给茶叶经销商,另一种方式是在各超市的柜台进行销售,每年该厂生产的茶叶都可以全部销售,该茶叶厂每年可以生产茶叶100万盒,其中,卖给茶叶经销商每盒茶叶的利润y1(元)与销售量x(万盒)之间的函数关系如图所示;在各超市柜台销售的每盒利润y2(元)与销售量x(万盒)之间的函数关系为:y2=$\left\{\begin{array}{l}{40(0≤x≤60)}\\{\frac{3}{4}x+5(60<x≤100)}\end{array}\right.$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线C1:y=mx2-2mx+m+4与y轴交于点A(0,3),与x轴交于点B、C(点B在点C左侧).
在平面直角坐标系xOy中,抛物线C1:y=mx2-2mx+m+4与y轴交于点A(0,3),与x轴交于点B、C(点B在点C左侧).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a(m-n)=d | B. | a(n-m)=d | C. | a(m-n)2=d | D. | a(m+n)2=d |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com