
【题目】四张完全相同的卡片上,分别画有圆、正方形、等边三角形和线段,现从中随机抽取两张,卡片上画的恰好都是中心对称图形的概率为( )
A.1
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:列表如下:
1 | 2 | 3 | 4 | |
1 | ﹣﹣﹣ | (2,1) | (3,1) | (4,1) |
2 | (1,2) | ﹣﹣﹣ | (3,2) | (4,2) |
3 | (1,3) | (2,3) | ﹣﹣﹣ | (4,3) |
4 | (1,4) | (2,4) | (3,4) | ﹣﹣﹣ |
其中1表示圆,2表示正方形,3表示等边三角形,4表示线段,
所有等可能情况数为12种,其中两张卡片上图形都是中心对称图形的有6种,
∴卡片上画的恰好都是中心对称图形的概率为 ![]() =
= ![]() ,
,
所以答案是:C.
【考点精析】关于本题考查的列表法与树状图法和概率公式,需要了解当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】一家商店进行门店升级需要装修,装修期间暂停营业,若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?
(3)装修完毕第二天即可正常营业,且每天仍可盈利200元(即装修前后每天盈利不变),你认为商店应如何安排施工更有利?说说你的理由.(可用(1)(2)问的条件及结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)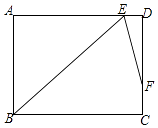
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y= ![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y= ![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB于D,点E为AC上一动点,过点E作EF⊥AB于F,连接DE.
(1)若∠1=∠2,求证:DE∥BC;
(2)在点E运动过程中,直线DE与直线BC交于点M,若∠DCB=α,∠M=β,则∠FED的度为 (用含α,β的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,D为AC中点,P为AB上的动点,将P绕点D逆时针旋转90°得到P′,连CP′,则线段CP′的最小值为 . 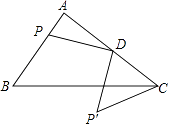
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至于30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题( ![]() )﹣1+
)﹣1+ ![]() +sin30°;
+sin30°;
(1)计算:( ![]() )﹣1+
)﹣1+ ![]() +sin30°;
+sin30°;
(2)先化简,再求值:(m+2)(m﹣2)﹣(m﹣2)2+1,其中m=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com