
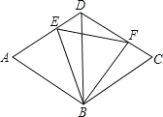
【题目】如图,边长为2的菱形ABCD中,BD=2,E、F分别是AD,CD上的动点(包含端点),且AE+CF=2,则线段EF长的最小值是__________.
【答案】![]()
【解析】
由在边长为2的菱形ABCD中,BD=2,易得△ABD、△CBD都是边长为2的正三角形,继而证得△BDE≌△BCF(SAS),继而证得△BEF是正三角形,继而可得当动点E运动到点D或点A时,BE的最大,当BE⊥AD,即E为AD的中点时,BE的最小.
∵四边形ABCD是边长为2的菱形,BD=2,
∴△ABD、△CBD都是边长为2的正三角形,
∵AE+CF=2,
∴CF=2AE=ADAE=DE,
又∵BD=BC=2,∠BDE=∠C=60,
DE=DF,∠BDE=∠C,BD=BC,
∴△BDE≌△BCF(SAS),
∴∠EBD=∠FBC,
∴∠EBD+∠DBF=∠FBC+∠DBF,
∴∠EBF=∠DBC=60,
又∵BE=BF,
∴△BEF是正三角形,
∴EF=BE=BF,
当BE⊥AD,即E为AD的中点时,BE的最小值为![]() ,
,
所以EF=BE=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
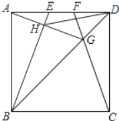
【题目】如图,正方形ABCD的边长为2cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H.点H在圆弧上运动上,点H所运动的圆弧的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )
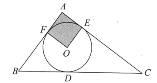
A.4B.6.25C.7.5D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
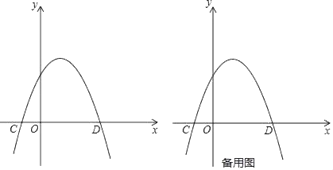
【题目】在平面直角坐标系![]() 中,规定:抛物线
中,规定:抛物线![]() 的伴随直线为
的伴随直线为![]() .例如:抛物线
.例如:抛物线![]() 的伴随直线为
的伴随直线为![]() ,即
,即![]() .
.
(1)在上面规定下,抛物线![]() 的顶点为 .伴随直线为 ;抛物线
的顶点为 .伴随直线为 ;抛物线![]() 与其伴随直线的交点坐标为 和 ;
与其伴随直线的交点坐标为 和 ;
(2)如图,顶点在第一象限的抛物线![]() 与其伴随直线相交于点
与其伴随直线相交于点![]() (点
(点![]() 在点
在点![]() 的右侧)与
的右侧)与![]() 轴交于点
轴交于点![]()
①若![]() 求
求![]() 的值;
的值;
②如果点![]() 是直线
是直线![]() 上方抛物线的一个动点,
上方抛物线的一个动点,![]() 的面积记为
的面积记为![]() ,当
,当![]() 取得最大值
取得最大值![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为正方形ABCD的对角线AC上的一点,连接BP并延长交CD于点E,交AD的延长线于点F,⊙O是△DEF的外接圆,连接DP.
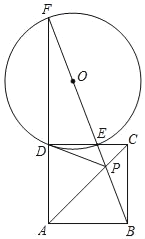
(1)求证:DP是⊙O的切线;
(2)若tan∠PDC=![]() ,正方形ABCD的边长为4,求⊙O的半径和线段OP的长.
,正方形ABCD的边长为4,求⊙O的半径和线段OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
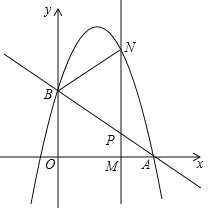
(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为线段OA上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
①试用含m的代数式表示线段PN的长;
②求线段PN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】面对突如其来的疫情,全国人民响应党和政府的号召,主动居家隔离.随之而来的,则是线上买菜需求激增.某小区为了解居民使用买菜APP的情况,通过制作无接触配送置物架,随机抽取了若干户居民进行调查(每户必选且只能选最常用的一个APP),现将调查结果绘制成如下两幅不完整的统计图:(A:天虹到家,B:叮咚买菜,C:每日优鲜,D:盒马鲜生)
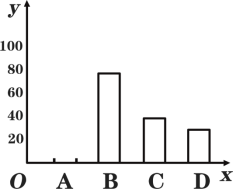
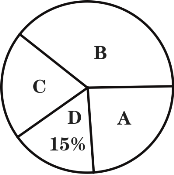
(1)本次随机调查了 户居民;
(2)补全条形统计图的空缺部分;
(3)若该小区共有1200户居民,请估计该小区居民选择“C:每日优鲜”的大约有 户;
(4)某日下午,张阿姨想购买苹果和生菜,各APP的供货情况如下:天虹到家仅有苹果在售,叮咚买菜仅有生菜在售,每日优鲜仅有生菜在售,盒马鲜生的苹果、生菜均已全部售完,则张阿姨随机选择两个不同的APP能买到苹果和生菜的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一方有难,八方支援”.四川汶川大地震牵动着全国人民的心,我市某医院准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士支援汶川.
(1)若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果;
(2)求恰好选中医生甲和护士A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
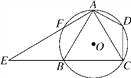
【题目】如图,已知四边形ABCD内接于⊙O,A是![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且![]() .
.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com