
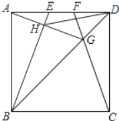
【题目】如图,正方形ABCD的边长为2cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H.点H在圆弧上运动上,点H所运动的圆弧的长为______.
【答案】![]()
【解析】
先根据全等三角形的性质证明∠AHB=90°,即点H是以AB为直径的圆上一点,再根据弧长公式求解即可得到答案.
∵ABCD是正方形
∴AD=CD=AB,∠BAD=∠ADC=90°,∠ADB=∠BDC=45°
∵AD=CD,∠ADB=∠BDC,DG=DG
∴△ADG≌△DGC
∴∠DAM=∠DCF且AD=CD,∠ADC=∠ADC
∴△ADM≌△CDF
∴FD=DM且AE=DF
∴AE=DM且AB=AD,∠ADM=∠BAD=90°
∴△ABE≌△ADM(SAS),
∴∠DAM=∠ABE,
∵∠DAM+∠BAM=90°,
∴∠BAM+∠ABE=90°,
即∠AHB=90°,
∴点H是以AB为直径的圆上一点,
以AB的中心O为圆心,以OA为半径画弧,与BD交于I,如图:
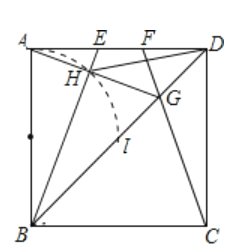
当E点运动到D的位置以及F点运动到A的位置时,是H运动的轨迹的一个端点,
此时,I刚好与H重合(恰好是正方形的中心),
∴此时的圆心角恰好是90°,
根据弧长公式得到H运动的弧长为:![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() .如果点
.如果点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,它们的速度分别为
匀速运动,它们的速度分别为![]() 和
和![]() .过点
.过点![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 和
和![]() ,设运动时间为
,设运动时间为![]()
![]() .
.
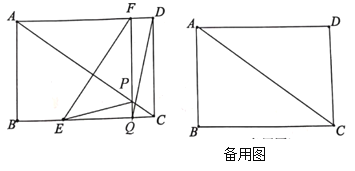
(1)连结![]() 、
、![]() ,若四边形
,若四边形![]() 为平行四边形,求
为平行四边形,求![]() 的值;
的值;
(2)连结![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求
的函数关系式,并求![]() 的最大值;
的最大值;
(3)若![]() 与
与![]() 相似,求出
相似,求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
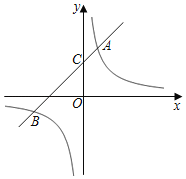
【题目】如图,在平面直角坐标系内xOy中,某一次函数的图象与反比例函数的y=![]() 的图象交于A(1,m)、B(n,﹣1)两点,与y轴交于C点.
的图象交于A(1,m)、B(n,﹣1)两点,与y轴交于C点.
(1)求该一次函数的解析式;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
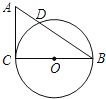
【题目】如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问:当点E在什么位置时,直线ED与⊙O相切?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,甲厂欲购买某种无纺布生产口罩,A、B两家无纺布公司各自给出了该种无纺布的销售方案.
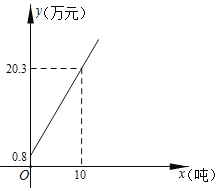
A公司方案:无纺布的价格y(万元)与其重量x(吨)是如图所示的函数关系;
B公司方案:无纺布不超过30吨时,每吨收费2万元;超过30吨时,超过的部分每吨收费1.9万元.
(1)求如图所示的y与x的函数解析式;(不要求写出定义域)
(2)如果甲厂所需购买的无纺布是40吨,试通过计算说明选择哪家公司费用较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
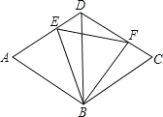
【题目】如图,边长为2的菱形ABCD中,BD=2,E、F分别是AD,CD上的动点(包含端点),且AE+CF=2,则线段EF长的最小值是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com