
【题目】如图,已知![]() 的半径为 4,
的半径为 4,![]() 是圆的直径,点
是圆的直径,点![]() 是
是![]() 的切线
的切线![]() 上的一个动点,连接
上的一个动点,连接![]() 交
交![]() 于点
于点![]() ,弦
,弦![]() 平行于
平行于![]() ,连接
,连接![]() .
.

(1)试判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当![]() __________时,四边形
__________时,四边形![]() 为菱形;
为菱形;
(3)当![]() ___________时,四边形
___________时,四边形![]() 为正方形.
为正方形.
【答案】【解析】(1)证明见解析;⑵60°;⑶![]() .
.
【解析】
(1)根据EF∥AB,可以得到∠FAB和∠CAB的关系,可证得△ACB≌△AFB,可求得∠AFB=90°,可得出结论;
(2)根据四边形ADFE为菱形,通过变形可以得到∠CAB的度数;
(3)根据四边形ACBF为正方形,AC=4,AF⊥AE且AF=AE,利用勾股定理可求得EF的长
(1)BF与⊙A相切,理由如下:
∵EF∥AB,
∴∠AEF=∠CAB,∠AFE=∠FAB,
又∵AE=AF,
∴∠AEF=∠AFE,
∴∠FAB=∠CAB,
在△ABC和△ABF中
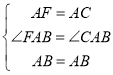
∴△ABC≌△ABF(SAS);
∴∠AFB=∠ACB =90°,
∴直线BF与⊙A相切.
(2)连接CF,如右图所示,
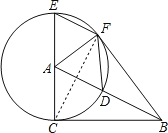
若四边形ADFE为菱形,则AE=EF=FD=DA,
又∵CE=2AE,CE是圆A的直径,
∴CE=2EF,∠CFE=90°,
∴∠ECF=30°,
∴∠CEF=60°,
∵EF∥AB,
∴∠AEF=∠CAB,
∴∠CAB=60°,
故答案为60°;
(3)若四边形ACBF为正方形,则AC=CB=BF=FA=4,且AF⊥AE,
∴![]()
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知点![]() ,线段
,线段![]() 与
与![]() 轴平行,且
轴平行,且![]() ,抛物线
,抛物线![]() (
(![]() 常数)经过点
常数)经过点![]()
(1)求![]() 的解析式及其对称轴和顶点坐标
的解析式及其对称轴和顶点坐标
(2)判断点![]() 是否在
是否在![]() 上,并说明理由;
上,并说明理由;
(3)若线段![]() 以每秒2个单位的速度向下平移,设平移的时间为
以每秒2个单位的速度向下平移,设平移的时间为![]() 秒
秒
①若![]() 与线段
与线段![]() 总有公共点,直接写出
总有公共点,直接写出![]() 的取值范围
的取值范围
②若![]() 同时以每秒3个单位的速度向下平移,
同时以每秒3个单位的速度向下平移,![]() 在
在![]() 轴及其右侧图像与直线
轴及其右侧图像与直线![]() 总有两个公共点,求
总有两个公共点,求![]() 的取值范围.
的取值范围.
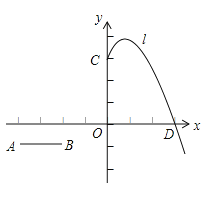
查看答案和解析>>
科目:初中数学 来源: 题型:
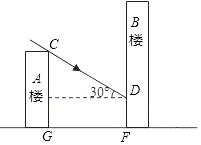
【题目】如图所示,小明家住在30米高的A楼里,小丽家住在B楼里,B楼坐落在A楼的正北面,已知当地冬至中午12时太阳光线与水平面的夹角为30°.
(1)如果A、B两楼相距16![]() 米,那么A楼落在B楼上的影子有多长?
米,那么A楼落在B楼上的影子有多长?
(2)如果A楼的影子刚好不落在B楼上,那么两楼的距离应是多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
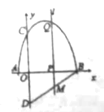
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() .
.
(1)求点![]() 、点
、点![]() 、点
、点![]() 的坐标;
的坐标;
(2)当点![]() 在线段
在线段![]() 上运动时,直线
上运动时,直线![]() 交
交![]() 于点
于点![]() ,试探究当
,试探究当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)在点![]() 的运动过程中,是否存在点
的运动过程中,是否存在点![]() ,使
,使![]() 是以
是以![]() 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
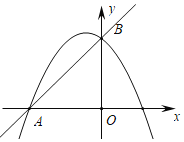
【题目】如图1,经过原点O的抛物线![]() (a≠0)与x轴交于另一点A(
(a≠0)与x轴交于另一点A(![]() ,0),在第一象限内与直线y=x交于点B(2,t).
,0),在第一象限内与直线y=x交于点B(2,t).
(1)求这条抛物线的表达式;
(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、
、![]() .
.
(1)求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的值.
的值.
(2)当![]() 时,若
时,若![]() 的函数值随
的函数值随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
(3)如图,当![]() 时,在抛物线上是否存在点
时,在抛物线上是否存在点![]() ,使
,使![]() 的面积为1?若存在,请求出符合条件的所有点
的面积为1?若存在,请求出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (a≠0)与x轴交于点A(﹣1,0)和点B(4,0).
(a≠0)与x轴交于点A(﹣1,0)和点B(4,0).
(1)求抛物线![]() 的函数解析式;
的函数解析式;
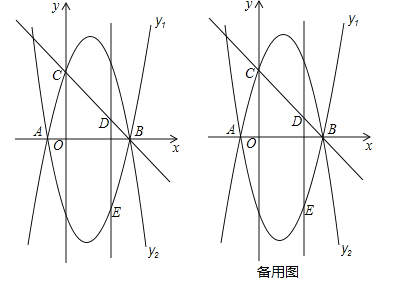
(2)如图①,将抛物线![]() 沿x轴翻折得到抛物线
沿x轴翻折得到抛物线![]() ,抛物线
,抛物线![]() 与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线
与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线![]() 于点E,求线段DE的长度的最大值;
于点E,求线段DE的长度的最大值;
(3)在(2)的条件下,当线段DE处于长度最大值位置时,作线段BC的垂直平分线交DE于点F,垂足为H,点P是抛物线![]() 上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.
上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了接受“省艺术特色学校”的验收,对义务教育的七、八、九三个年级学生举行了书法大赛,赛后对三个年级的获奖情况进行了统计,并绘制了如图所示的两幅不完整的统计图.
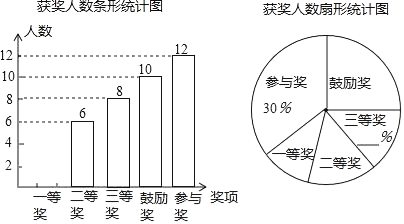
请解答下列问题:
(1)请补全两幅统计图;
(2)获得一等奖的同学有![]() 来自七年级,有
来自七年级,有![]() 来自八年级,其余同学均来自九年级.现准备从获得一等奖的同学中任选两人参加市内书法大赛,请你通过列表或画树状图,求所选两人中既有八年级同学又有九年级同学的概率.
来自八年级,其余同学均来自九年级.现准备从获得一等奖的同学中任选两人参加市内书法大赛,请你通过列表或画树状图,求所选两人中既有八年级同学又有九年级同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=-2x+12分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的⊙M与直线AB相切于点D,连接MD.
(1)求证:△ADM∽△AOB.
(2)如果⊙M的半径为2![]() ,请写出点M的坐标,并写出以点
,请写出点M的坐标,并写出以点![]() 为顶点,且过点M的抛物线的函数表达式.
为顶点,且过点M的抛物线的函数表达式.
(3)在(2)的条件下,试问在此抛物线上是否存在点P,使以P,A,M三点为顶点的三角形与△AOB相似?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com