
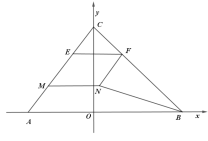
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() ,E,M为线段AC上两个不重合的动点(点E在点M上方,且均不与端点重合),
,E,M为线段AC上两个不重合的动点(点E在点M上方,且均不与端点重合),![]() ,与BC交于点F,四边形EMNF为平行四边形,连结BN.
,与BC交于点F,四边形EMNF为平行四边形,连结BN.
(1)求直线AC与直线BC的解析式;
(2)若设点F的横坐标为x,点M的纵坐标为y,当四边形EMNF为菱形时,请求y关于x的函数解析式及相应x的取值范围;
(3)请求出当![]() 为等腰三角形时,
为等腰三角形时,![]() 面积的最大值.
面积的最大值.
【答案】(1)直线AC解析式为![]() ,直线BC解析式为
,直线BC解析式为![]() ;
;
(2)y关于x的函数解析式为![]() ,x的取值范围为
,x的取值范围为![]() ;
;
(3)![]() .
.
【解析】
(1)待定系数法求解析式即可;
(2)利用邻边相等的平行四边形是菱形的性质,用字母把邻边表示出来求解即可;
(3)首先判断等腰三角形的可能性,大胆设出F,N的坐标,列出平行四边形的面积的函数,根据二次函数的性质求最大面积.
解:(1) 设直线AC解析式为:![]() ,将
,将![]() ,
,![]() 代入得,
代入得,
 解得
解得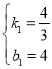
所以,直线AC解析式为![]() .
.
设直线BC解析式为:![]() ,将
,将![]() ,
,![]() 代入得,
代入得,
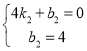 解得
解得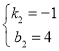
所以,直线BC解析式为![]() .
.
(2)![]() 点F的横坐标为x,且F在直线BC上,
点F的横坐标为x,且F在直线BC上,
![]()
![]() 点M的纵坐标为y,且M在直线AC上,
点M的纵坐标为y,且M在直线AC上,
![]()
![]()
![]()
![]() E、F的纵坐标相同,又E在直线AC上,
E、F的纵坐标相同,又E在直线AC上,
![]()
![]() 四边形EMNF为菱形,
四边形EMNF为菱形,
![]()
![]()
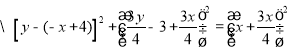
整理得:![]()
![]() E在M上方,即E点纵坐标大于M点纵坐标,
E在M上方,即E点纵坐标大于M点纵坐标,
![]() 即
即![]()
又![]()
![]() 对
对![]() 两边进行开方得,
两边进行开方得,![]()
整理得:![]()
由题知,![]() ,即
,即![]()
解得![]()
![]() y关于x的函数解析式为
y关于x的函数解析式为![]() ,x的取值范围为
,x的取值范围为![]() .
.
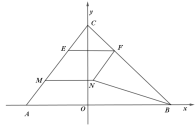
(3)由题意当![]() 或
或![]() 时,点N在
时,点N在![]() 外,不符合题意,
外,不符合题意,
当![]() 时,作
时,作![]() 交EF于点D,
交EF于点D,
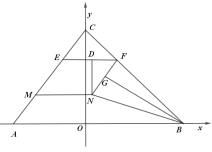
设![]() ,
,![]() ,
,
易得![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]()
设FN中点为点G,又![]() ,
,
![]() ,
,
∵在△BNF中![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
 ,
,
解得![]() ,
,
由题意![]() ,
,
当![]() 时,
时,![]() 的面积有最大值,
的面积有最大值,
此时![]() .
.


科目:初中数学 来源: 题型:
【题目】某公司生产一种健身产品在市场上很受欢迎,该公司每年的产量为6万件,可在国内和国外两个市场全部销售.若在国外销售,平均每件产品的利润y1(元)与国外销售量x(万件)的函数关系式为y1=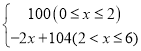 .若在国内销售,平均每件产品的利润为y2=84元.
.若在国内销售,平均每件产品的利润为y2=84元.
(1)求该公司每年在国内和国外销售的总利润w(万元)与国外销售量x(万件)的函数关系式,并指出x的取值范围;
(2)该公司每年在国内国外销售量各为多少时,可使公司每年的总利润最大?最大值是多少?
(3)该公司计划从国外销售的每件产品中捐出2m(1≤m≤4)元给希望工程,从国内销售的每件产品中捐出m元给希望工程,且国内销售不低于4万件,若这时国内国外销售的总利润的最大值为520万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+bx+c的图象经过坐标原点O和点A(7,0),直线AB交y轴于点B(0,﹣7),动点C(x,y)在直线AB上,且1<x<7,过点C作x轴的垂线交抛物线于点D,则CD的最值情况是( )
A.有最小值9B.有最大值9C.有最小值8D.有最大值8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答下列问题:
材料一:一个三位以上的自然数,如果该自然数的末三位表示的数与末三位之前的数字表示的数之差是11的倍数,我们称满足此特征的数叫“网红数”,如:65362,362﹣65=297=11×27,称65362是“网红数”.
材料二:对任的自然数p均可分解为P=100x+10y+z(x≥0,0≤y≤9,0≤z≤9且x、y,z均为整数)如:5278=52×100+10×7+8,规定:G(P)=![]() .
.
(1)求证:任两个“网红数”之和一定能被11整除;
(2)已知:S=300+10b+a,t=1000b+100a+1142(1≤a≤7,0≤b≤5,其a、b均为整数),当s+t为“网红数”时,求G(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
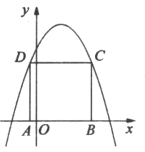
【题目】如图,在平面直角坐标系![]() 中,A、B为x轴上的点,C、D为抛物线y=-x2+2x+3上两点,且四边形ABCD是正方形,则正方形ABCD的面积是__________.
中,A、B为x轴上的点,C、D为抛物线y=-x2+2x+3上两点,且四边形ABCD是正方形,则正方形ABCD的面积是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
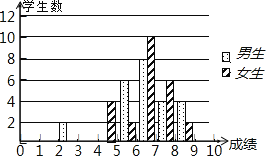
【题目】为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
男生 | 6.9 | 2.4 | ______ | 91.7% | 16.7% |
女生 | ______ | 1.3 | ______ | 83.3% | 8.3% |
(2)男生说他们的合格率、优秀率均高于女生,所以他们的成绩好于女生,但女生不同意男生的说法,认为女生的成绩要好于男生,请给出两条支持女生观点的理由;
(3)体育老师说,咱班的合格率基本达标,但优秀率太低,我们必须加强体育锻炼,两周后的目标是:全班优秀率达到50%.如果女生新增优秀人数恰好是男生新增优秀人数的两倍,那么男、女生分别新增多少优秀人数才能达到老师的目标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC所在平面上的动点,连接OB,OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.

(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,点O所在位置应满足什么条件?(直接写出答案不需要说明理由.)
(3)在图2中作出点O,使得四边形DGFE是正方形(保留作图痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
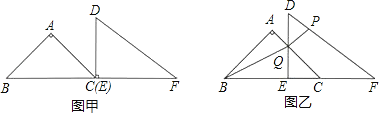
【题目】已知:把Rt△ABC和Rt△DEF按如图甲摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠BAC=∠DEF=90°,∠ABC=45°,BC=9cm,DE=6cm,EF=8cm.如图乙,△DEF从图甲的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△DEF的顶点F出发,以3cm/s的速度沿FD向点D匀速移动.当点P移动到点D时,P点停止移动,△DEF也随之停止移动.DE与AC相交于点Q,连接BQ、PQ,设移动时间为t(s).解答下列问题:
(1)设三角形BQE的面积为y(cm2),求y与t之间的函数关系式,并写出自变量t的取值范围;
(2)当t为何值时,三角形DPQ为等腰三角形?
(3)是否存在某一时刻t,使P、Q、B三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com