
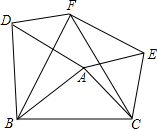
 如图,以△ABC各边向同一侧作三个等边三角形△ABD,△ACE,△BCF.
如图,以△ABC各边向同一侧作三个等边三角形△ABD,△ACE,△BCF.
|

| 1 |
| 2 |


科目:初中数学 来源: 题型:
| A、900元 |
| B、1 000元 |
| C、960元 |
| D、980元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 家庭 类型 |
贫困 家庭 |
温饱 家庭 |
小康 家庭 |
富裕 家庭 |
最富裕 家庭 |
| 恩格尔 系数n |
0.60<n | 0.50≤n≤0.60 | 0.40≤n≤0.49 | 0.30≤n≤0.39 | n<0.30 |
| 家庭日常饮食开支 |
| 家庭总支出 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某校对学生的上学方式进行一次抽样调查,结果为如图绘制成的扇形统计图.已知该校学生共有2 560人,被调查的学生中骑车的有21人,求:
某校对学生的上学方式进行一次抽样调查,结果为如图绘制成的扇形统计图.已知该校学生共有2 560人,被调查的学生中骑车的有21人,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com