
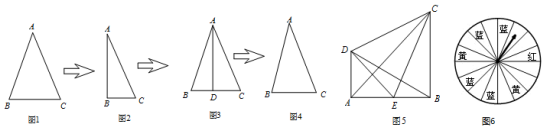
分析 归纳结论:作等腰三角形底边上的高,构造全等三角形.
探究应用:(1)BE与AD在两个直角三角形中,证这两个直角三角形全等即可;
(2)可证点A,C在线段DE的垂直平分线上.注意结合(1)的结论,利用全等证明即可;
(3)由第二问的垂直平分线的性质,得到CD=CE,由第一问的全等得到DB=CE,那么CD=BD,所以∠DBC=∠DCB;
(4)①找到红色区域的份数占总份数的多少即为获得一等奖的概率,
②游戏是否合算,关键要看游戏双方获胜的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
解答 解:思考验证: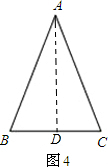
过A点作AD⊥BC于D,
∴∠ADB=∠ADC=90°,
在Rt△ABD和Rt△ACD中,$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△ACD(HL),
∴∠B=∠C;
探究应用: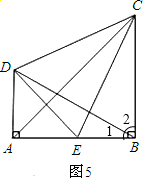
(1)说明:因为BD⊥EC,
∴∠CEB+∠1=90°,
∠1+∠ADB=90°,
∴∠ADB=∠BEC,
在△ADB和△BEC中$\left\{\begin{array}{l}{∠ADB=∠BEC}\\{AB=BC}\\{∠DAB=∠EBC=90°}\end{array}\right.$,
∴△DAB≌△EBC(ASA).
∴DA=BE.
(2)∵E是AB中点,
∴AE=BE.
∵AD=BE,
∴AE=AD.
在△ABC中,因为AB=BC,
∴∠BAC=∠BCA.
∵AD∥BC,
∴∠DAC=∠BCA.
∴∠BAC=∠DAC.
在△ADC和△AEC中,$\left\{\begin{array}{l}{AD=AE}\\{∠DAC=∠EAC}\\{AC=AC}\end{array}\right.$,
∴△ADC≌△AEC(SAS).
∴DC=CE.
∴C在线段DE的垂直平分线上.
∵AD=AE,
∴A在线段DE的垂直平分线上.
∴AC垂直平分DE.
(3)∵AC是线段DE的垂直平分线,
∴CD=CE.
∵△ADB≌△BEC,
∴DB=CE.
∴CD=BD.
∴∠DBC=∠DCB;
(4)①整个圆周被分成了16份,红色为1份,
∴获得一等奖的概率为:$\frac{1}{16}$,
②转转盘:60×$\frac{1}{16}$+50×$\frac{2}{16}$+40×$\frac{4}{16}$=20元,
∵20元>15元,
∴转转盘划算.
点评 此题是三角形综合题,主要考查了全等三角形的判定和性质,等腰直角三角形的判定和性质,解本题的关键是作出作∠BAC的角平分线AD判断∠B=∠C.


科目:初中数学 来源: 题型:解答题
| 您的最主要阅读载体(限选一种) | ||||
| A.手机 | B.电脑 | C.电子书 | D.纸质书 | E.其他 |
| 45 | 30 | 75 | 130 | 10 |
| 您阅读过书的类型(可多选) | |||
| A.历史传记类 | B.社会哲学类 | C.科普科技类 | D.文学名著类 |
| 236 | 35 | 185 | 290 |
| E.报刊杂志类 | F.网络小说类 | G.漫画类 | H.其他160 |
| 216 | 85 | 196 | 160 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com