
【题目】已知抛物线![]() 的对称轴是直线
的对称轴是直线![]() 且与
且与![]() 轴相交于
轴相交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点
若点![]() 是第一象限内抛物线上一点,过点
是第一象限内抛物线上一点,过点![]() 作直线
作直线![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() 当
当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.
![]() 在
在![]() 的条件下,若点
的条件下,若点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,当以点
在抛物线的对称轴上,当以点![]() 为顶点的四边形是平行四边形时,求出所有符合条件的点
为顶点的四边形是平行四边形时,求出所有符合条件的点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)满足条件的点
;(3)满足条件的点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]()
【解析】
(1)根据抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,点
,点![]() 在抛物线上,列出方程组,求得
在抛物线上,列出方程组,求得![]() 中字母的值,即可得到抛物线的解析式.
中字母的值,即可得到抛物线的解析式.
(2)先根据抛物线的解析式,得到点![]() 、点
、点![]() 的坐标;再由点
的坐标;再由点![]() 、点
、点![]() 的坐标,得到直线
的坐标,得到直线![]() 的解析式;设点
的解析式;设点![]() 的坐标为
的坐标为![]() ,得
,得![]() ,
,![]() ,根据已知条件
,根据已知条件![]() ,列出方程,通过解方程求得未知数,得到
,列出方程,通过解方程求得未知数,得到![]() 、
、![]() ,
,![]() 三点坐标,根据三角形面积公式,结合图1,利用割补法求面积,即有
三点坐标,根据三角形面积公式,结合图1,利用割补法求面积,即有![]() ,即可得到答案.
,即可得到答案.
(3)设点![]() 的坐标为
的坐标为![]() ,分三种情况进行讨论:
,分三种情况进行讨论:![]() 如图2,当
如图2,当![]() 为对角线时,点
为对角线时,点![]() 的坐标为
的坐标为![]() ;
;![]() 如图3,当
如图3,当![]() 为对角线时,点
为对角线时,点![]() 的坐标为
的坐标为![]() ;
;![]() 如图4.当
如图4.当![]() 为对角线时,点
为对角线时,点![]() 的坐标为
的坐标为![]() ,分别将点
,分别将点![]() 的坐标代入
的坐标代入![]() ,即得到三个不同的点
,即得到三个不同的点![]() .
.
解:(1)∵点![]() 的坐标为
的坐标为![]() ,对称轴是直线
,对称轴是直线![]() ,
,
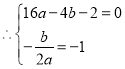
解得![]()
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
(2)画出图形,如图1所示,
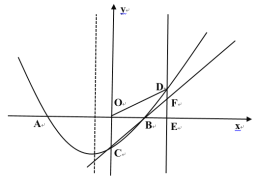
图1
令![]() ,代入
,代入![]() ,
,
解得![]() ,
,![]() ,
,
∵点![]() 的坐标为
的坐标为![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
令![]() ,代入
,代入![]() ,得
,得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
可求得直线![]() 的解析式为
的解析式为![]() .
.
设点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ,
,
∴![]() .
.
(3)设点![]() 的坐标为
的坐标为![]() ,
,
![]() 如图2,当
如图2,当![]() 为对角线时,点
为对角线时,点![]() 的坐标为
的坐标为![]() ,
,
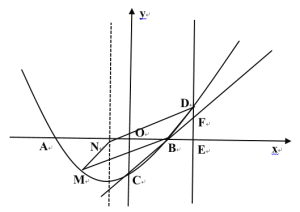
图2
将点![]() 坐标代入
坐标代入![]() 得,
得,![]() ,
,
此时点![]() 的坐标为
的坐标为![]() ;
;
![]() 如图3,当
如图3,当![]() 为对角线时,点
为对角线时,点![]() 的坐标为
的坐标为![]() ,
,
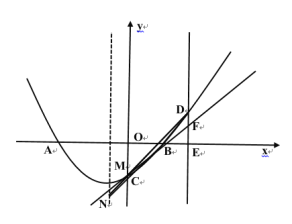
图3
将点![]() 坐标代入
坐标代入![]() 得,
得, ![]() ,
,
此时点![]() 的坐标为
的坐标为![]() ;
;
![]() 如图4.当
如图4.当![]() 为对角线时,点
为对角线时,点![]() 的坐标为
的坐标为![]() ,
,
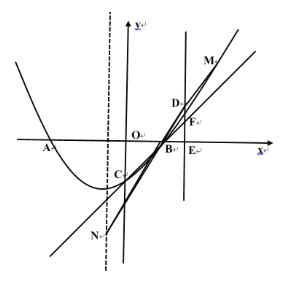
图4
将点![]() 坐标代入
坐标代入![]() 得,
得,![]() ,
,
此时点![]() 的坐标为
的坐标为![]() .
.
综上所述,满足条件的点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
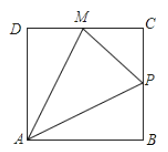
【题目】如图,点P按A→B→C→M的顺序在边长为l的正方形边上运动,M是CD边上中点,设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图像是( )
A.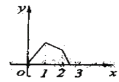 B.
B. C.
C.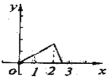 D.
D.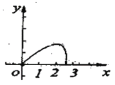
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.1 |
70≤x<80 | 90 | n |
80≤x<90 | m | 0.4 |
90≤x≤100 | 60 | 0.2 |

请根据以上图表提供的信息,解答下列问题:
(1)本次调查的样本容量为 ;
(2)在表中:m= .n= ;
(3)补全频数分布直方图:
(4)参加比赛的小聪说,他的比赛成绩是所有抽查同学成绩的中位数,据此推断他的成绩落在 分数段内;
(5)如果比赛成绩80分以上(含80分)为优秀,那么你估计该竞赛项目的优秀率大约是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校九年级学生的课外数学学习时长情况,该校将选取部分学生进行调查,以下样本中,最具代表性的是( )
A.该年级篮球社团的学生
B.该年级数学成绩前![]() 名的女生
名的女生
C.该年级跑步较快的学生
D.从每个班级中,抽取学号为![]() 的整数倍的学生
的整数倍的学生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB∥x轴,AB=6.点A的坐标为(1,﹣4),点D的坐标为(﹣3,4),点B在第四象限,点G是AD与y轴的交点,点P是CD边上不与点C,D重合的一个动点,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+4x+5图象的顶点为D,对称轴是直线1,一次函数y![]() x+1的图象与x轴交于点A,且与直线DA关于l的对称直线交于点B.
x+1的图象与x轴交于点A,且与直线DA关于l的对称直线交于点B.
(1)点D的坐标是 ;
(2)直线l与直线AB交于点C,N是线段DC上一点(不与点D、C重合),点N的纵坐标为n.过点N作直线与线段DA、DB分别交于点P、Q,使得△DPQ与△DAB相似.
①当n![]() 时,求DP的长;
时,求DP的长;
②若对于每一个确定的n的值,有且只有一个△DPQ与△DAB相似,请直接写出n的取值范围 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 交于点
交于点![]() ,将点
,将点![]() 向右平移某个距离得到点
向右平移某个距离得到点![]() ,点
,点![]() 在抛物线上.已知点
在抛物线上.已知点![]() ,
,![]() .
.
(1) 当![]() 时.
时.
①求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
②求线段![]() 的长度;
的长度;
(2)若抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
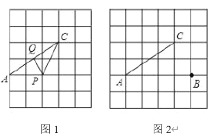
【题目】在每个小正方形的边长为1的网格中,点![]() ,
,![]() ,
,![]() 均在格点上,点
均在格点上,点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点.
上的动点.
(I)如图(1),当点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点时,
中点时,![]() 的值为__________;
的值为__________;
(Ⅱ)当![]() 取得最小值时,在如图(2)所示的网格中,用无刻度的真尺,画出线段
取得最小值时,在如图(2)所示的网格中,用无刻度的真尺,画出线段![]() ,
,![]() ,简要说明点
,简要说明点![]() 和点
和点![]() 的位置是如何找到的(不要求证明)__________.
的位置是如何找到的(不要求证明)__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com