
【题目】已知二次函数y=ax+bx-4(a,b是常数.且a![]() 0)的图象过点(3,-1).
0)的图象过点(3,-1).
(1)试判断点(2,2-2a)是否也在该函数的图象上,并说明理由.
(2)若该二次函数的图象与x轴只有一个交点,求该函数表达式.
(3)已知二次函数的图像过(![]() ,
,![]() )和(
)和(![]() ,
,![]() )两点,且当
)两点,且当![]() <
<![]()
![]()
![]() 时,始终都有
时,始终都有![]() >
>![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)不在;(2)![]() ;
;![]() ;(3)
;(3)![]()
【解析】
(1)将点![]() 代入函数解析式,求出a和b的等式,将函数解析式改写成只含有a的形式,再将点
代入函数解析式,求出a和b的等式,将函数解析式改写成只含有a的形式,再将点![]() 代入验证即可;
代入验证即可;
(2)令![]() ,得到一个一元二次方程,由题意此方程只有一个实数根,由根的判别式即可求出a的值,从而可得函数表达式;
,得到一个一元二次方程,由题意此方程只有一个实数根,由根的判别式即可求出a的值,从而可得函数表达式;
(3)根据函数解析式求出其对称轴,再根据函数图象的增减性判断即可.
(1)![]() 二次函数图像过点
二次函数图像过点![]()
![]() 代入得
代入得![]() ,
,![]()
![]() ,代入得
,代入得![]()
将![]() 代入得
代入得![]() ,得
,得![]() ,不成立,所以点
,不成立,所以点![]() 不在该函数图像上;
不在该函数图像上;
(2)由(1)知,![]()
![]() 与x轴只有一个交点
与x轴只有一个交点
![]() 只有一个实数根
只有一个实数根
![]() ,
,![]() 或
或![]()
当![]() 时,
时,![]() ,所以表达式为:
,所以表达式为:![]()
当![]() 时,
时,![]() ,所以表达式为:
,所以表达式为:![]() ;
;
(3)![]()
![]()
![]() 对称轴为
对称轴为![]()
当![]() 时,函数图象如下:
时,函数图象如下:
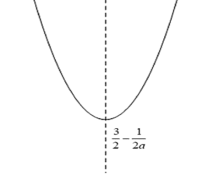
若要满足![]() 时,
时,![]() 恒大于
恒大于![]() ,则
,则![]() 、
、![]() 均在对称轴左侧
均在对称轴左侧
![]() ,
,![]()
当![]() 时,函数图象如下:
时,函数图象如下:
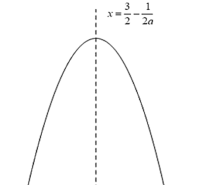
![]() ,此时
,此时![]() ,
,![]() 必小于
必小于![]()
综上,所求的a的取值范围是:![]() .
.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,双曲线y=![]() (k≠0)与直线y=ax+b(a≠0)交于A,B两点,直线AB分别交x轴,y轴于C、D两点,若OA=OC,A点坐标为(4,3).
(k≠0)与直线y=ax+b(a≠0)交于A,B两点,直线AB分别交x轴,y轴于C、D两点,若OA=OC,A点坐标为(4,3).
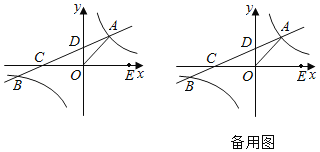
(1)分别求出双曲线与直线的函数表达式;
(2)若P为双曲线上一点,且横坐标为2,H为直线AB上一点,且PH+![]() HC最小,延长PH交x轴于点E,将线段OE沿x轴平移得线段O'E',在平移过程中,是否存在某个位置使|BO'﹣AE'|的值最大值,求出最大值并求出此时E点坐标.
HC最小,延长PH交x轴于点E,将线段OE沿x轴平移得线段O'E',在平移过程中,是否存在某个位置使|BO'﹣AE'|的值最大值,求出最大值并求出此时E点坐标.
(3)在(2)的情况下,将直线OA沿线段CE平移,平移过程中交y=![]() (x>0)的图象于M(M与点A不重合)交x轴于点N,在平面内找一点G,使M、N,E,G为顶点的四边形为矩形?直接写出G的坐标.
(x>0)的图象于M(M与点A不重合)交x轴于点N,在平面内找一点G,使M、N,E,G为顶点的四边形为矩形?直接写出G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。
(1)将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】岳阳市整治农村“空心房”新模式,获评全国改革开放40年地方改革创新40案例.据了解,我市某地区对辖区内“空心房”进行整治,腾退土地1200公顷用于复耕和改造,其中复耕土地面积比改造土地面积多600公顷.
(1)求复耕土地和改造土地面积各为多少公顷;
(2)该地区对需改造的土地进行合理规划,因地制宜建设若干花卉园和休闲小广场,要求休闲小广场总面积不超过花卉园总面积的![]() ,求休闲小广场的总面积最多为多少公顷.
,求休闲小广场的总面积最多为多少公顷.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
![]() 求出每天的销售利润
求出每天的销售利润![]() 元
元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
![]() 如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?
如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?![]() 每天的总成本
每天的总成本![]() 每件的成本
每件的成本![]() 每天的销售量
每天的销售量![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ABC=90°,点D在AC上,将△ABD绕顶点B沿顺时针方向旋转90°后得到△CBE.
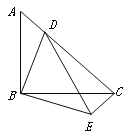
(1)求∠DCE的度数;
(2)当AB=4,AD∶DC=1∶3时,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com