
【题目】如图,在平面直角坐标系中,矩形OACB的顶点O是坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E为边OA上的一个动点,当△CDE的周长最小时,则点E的坐标____________.
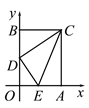
【答案】(1,0)
【解析】分析:由于C、D是定点,则CD是定值,如果![]() 的周长最小,即
的周长最小,即![]() 有最小值.为此,作点D关于x轴的对称点D′,当点E在线段CD′上时
有最小值.为此,作点D关于x轴的对称点D′,当点E在线段CD′上时![]() 的周长最小.
的周长最小.
详解:
如图,作点D关于x轴的对称点D′,连接CD′与x轴交于点E,连接DE.
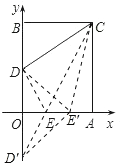
若在边OA上任取点E′与点E不重合,连接CE′、DE′、D′E′
由DE′+CE′=D′E′+CE′>CD′=D′E+CE=DE+CE,
可知△CDE的周长最小,
∵在矩形OACB中,OA=3,OB=4,D为OB的中点,
∴BC=3,D′O=DO=2,D′B=6,
∵OE∥BC,
∴Rt△D′OE∽Rt△D′BC,有![]()
∴OE=1,
∴点E的坐标为(1,0).
故答案为:(1,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
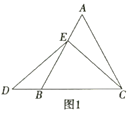
【题目】数学课上,李老师出示了如下的题目:如图1,在等边![]() 中,点
中,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,试确定线段
,试确定线段![]() 与
与![]() 的大小关系,并说明理由,
的大小关系,并说明理由,
(1)小敏与同桌小聪探究解答的思路如下:
①特殊情况,探索结论,
当点![]() 为
为![]() 的中点时,如图2,确定线段
的中点时,如图2,确定线段![]() 与
与![]() 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:![]() ______
______![]() .(填>,<或=)
.(填>,<或=)
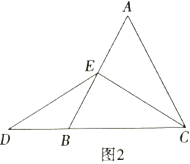
②特例启发,解答题目,
解:题目中,![]() 与
与![]() 的大小关系是:
的大小关系是:![]() ______
______![]() .(填>,<或=)
.(填>,<或=)
理由如下:如图3,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,(请你补充完成解答过程)
,(请你补充完成解答过程)
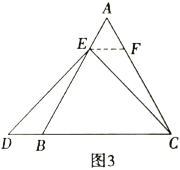
(2)拓展结论,设计新题,
同学小敏解答后,提出了新的问题:在等边![]() 中,点
中,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() ,已知
,已知![]() 的边长为
的边长为![]() ,求
,求![]() 的长?(请直接写出结果)
的长?(请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小岛在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正东方向.求货船的航行速度.(精确到0.1海里/时,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
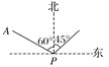
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠APB=30°,OP=3cm,⊙O的半径为1cm,若圆心O沿着BP的方向在直线BP上移动.(1)当圆心O移动的距离为1cm时,则⊙O与直线PA的位置关系是_____.(2)若圆心O的移动距离是d,当⊙O与直线PA相交时,则d的取值范围是_____.
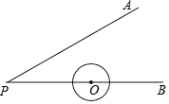
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上运动(不与点
上运动(不与点![]() 重合).
重合).
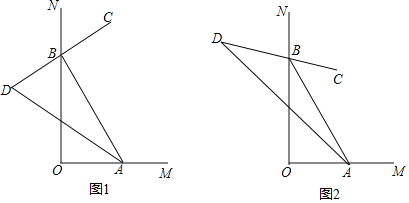
(1)如图1,![]() 是
是![]() 的平分线,
的平分线,![]() 的反方向延长线与
的反方向延长线与![]() 的平分线交于点
的平分线交于点![]() .
.
①若![]() ,则
,则![]() 为多少度?请说明理由.
为多少度?请说明理由.
②猜想:![]() 的度数是否随
的度数是否随![]() 、
、![]() 的移动发生变化?请说明理由.
的移动发生变化?请说明理由.
(2)如图2,若![]() ,
,![]() ,则
,则![]() 的大小为 度(直接写出结果);
的大小为 度(直接写出结果);
(3)若将“![]() ”改为“
”改为“![]() (
(![]() )”,且
)”,且![]() ,
,![]() ,其余条件不变,则
,其余条件不变,则![]() 的大小为 度(用含
的大小为 度(用含![]() 、
、![]() 的代数式直接表示出米).
的代数式直接表示出米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边上的中线,点D,E分别在边AC和BC上,DB=DE,DE与BM相交于点N,EF⊥AC于点F,以下结论:
①∠DBM=∠CDE;②S△BDE<S四边形BMFE;③CD·EN=BN·BD;④AC=2DF.
其中正确结论的个数是( )
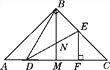
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
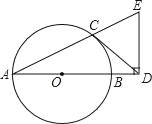
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com