
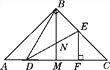
【题目】如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边上的中线,点D,E分别在边AC和BC上,DB=DE,DE与BM相交于点N,EF⊥AC于点F,以下结论:
①∠DBM=∠CDE;②S△BDE<S四边形BMFE;③CD·EN=BN·BD;④AC=2DF.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】试题分析:由AB=BC,∠ABC=90°,BM是AC边中线可知△ABC、△ABM、△CBM都是等腰直角三角形,因为DB=DE,所以对应两个底角相等.(1)∵∠DEB=∠EDC+∠C=∠EDC+45°(三角形外角性质),∴∠EDC=∠DEB-45°,因为∠DBE=∠DBM+∠MBE=∠DBM+45°,所以∠DBM=∠DBE-45°,而∠DBE=∠DEB,∴∠DBM=∠CDE,故(1)正确.(2)先证明△BDM≌△DEF,∵∠DBM=∠EDF(已证),∠DMB=∠EFD=90°,DB=DE,∴Rt△BDM≌Rt△DEF.∴S△BDM=S△DEF.∴S△BDM﹣S△DMN=S△DEF﹣S△DMN,即S△DBN=S四边形MNEF.∴S△DBN+S△BNE=S四边形MNEF+S△BNE,即S△BDE=S四边形BMFE,故(2)错误;(3)由所给CDEN=BNBD,化成比例式:CD:BD=BN:EN,所以只要能证明△DBC∽△NEB即可.∵∠BNE=∠DBM+∠BDN(三角形外角性质),∠BDM=∠BDE+∠EDF,∠EDF=∠DBM,∴∠BNE=∠BDM.即∠BNE=∠BDC,又∵∠C=∠NBE=45°,∴△DBC∽△NEB.∴对应线段成比例CD:BD=BN:EN,化成乘积式即得CDEN=BNBD,故(3)正确;(4)把所给线段进行转换:∵Rt△BDM≌Rt△DEF,∴BM=DF,∵BM是等腰直角三角形ABC斜边AC中线,∴BM=![]() AC,∴DF=
AC,∴DF=![]() AC,∴AC=2DF.故(4)正确.综上所述,选项中有三个正确,故选C.
AC,∴AC=2DF.故(4)正确.综上所述,选项中有三个正确,故选C.


科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() .动点
.动点![]() 从
从![]() 的顶点
的顶点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 匀速运动回到点
匀速运动回到点![]() .图2是点
.图2是点![]() 运动过程中,线段
运动过程中,线段![]() 的长度
的长度![]() 随时间
随时间![]() 变化的图象.其中点
变化的图象.其中点![]() 为曲线部分的最低点.
为曲线部分的最低点.
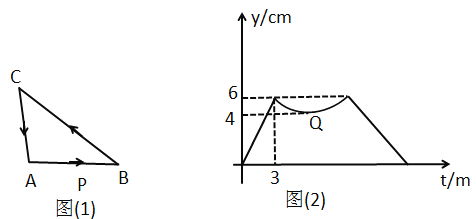
请从下面A、B两题中任选一作答,我选择________题.
A.![]() 的面积是______,B.图2中
的面积是______,B.图2中![]() 的值是______.
的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
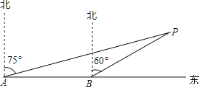
【题目】已知:如图,为了躲避台风,一轮船一直由西向东航行,上午![]() 点,在
点,在![]() 处测得小岛
处测得小岛![]() 的方向是北偏东
的方向是北偏东![]() ,以每小时
,以每小时![]() 海里的速度继续向东航行,中午
海里的速度继续向东航行,中午![]() 点到达
点到达![]() 处,并测得小岛
处,并测得小岛![]() 的方向是北偏东
的方向是北偏东![]() ,若小岛周围
,若小岛周围![]() 海里内有暗礁,问该轮船是否能一直向东航行?
海里内有暗礁,问该轮船是否能一直向东航行?
查看答案和解析>>
科目:初中数学 来源: 题型:
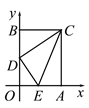
【题目】如图,在平面直角坐标系中,矩形OACB的顶点O是坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E为边OA上的一个动点,当△CDE的周长最小时,则点E的坐标____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新春佳节,电子鞭炮因其安全、无污染开始走俏.某商店经销一种电子鞭炮,已知这种电子鞭炮的成本价为每盒80元,市场调查发现,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种电子鞭炮销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)该商店销售这种电子鞭炮要想每天获得2400元的销售利润,又想买得快.那么销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
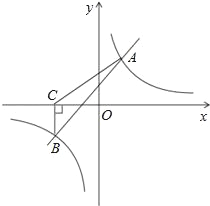
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(2,3),B(﹣3,n)两点.
的图象相交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a、b、c都是常数,且a≠0)的图象与x轴交于点(﹣2,0)、(x1,0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方,下列结论:①4a﹣2b+c=0;②a<b<0;③2a+c>0;④2a﹣b+1>0.其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬学生爱国主义精神,充分展现新时期青少年良好的思想道德素质和精神风貌,丰富学生的校园生活,陶冶师生的情操,某校举办了“中国梦爱国情成才志”中华经典诗文诵读比赛.九(1)班通过内部初选,选出了丽丽和张强两位同学,但学校规定每班只有1个名额,经过老师与同学们商量,用所学的概率知识设计摸球游戏决定谁去,设计的游戏规则如下:在A、B两个不透明的箱子分别放入黄色和白色两种除颜色外均相同的球,其中A箱中放置3个黄球和2个白球;B箱中放置1个黄球,3个白球,丽丽从A箱中摸一个球,张强从B箱摸一个球进行试验,若两人摸出的两球都是黄色,则丽丽去;若两人摸出的两球都是白色,则张强去;若两人摸出球颜色不一样,则放回重复以上动作,直到分出胜负为止.
根据以上规则回答下列问题:
(1)求一次性摸出一个黄球和一个白球的概率;
(2)判断该游戏是否公平?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com