
【题目】已知二次函数y=ax2+bx+c(a、b、c都是常数,且a≠0)的图象与x轴交于点(﹣2,0)、(x1,0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方,下列结论:①4a﹣2b+c=0;②a<b<0;③2a+c>0;④2a﹣b+1>0.其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
根据待定系数法、方程根与系数的关系等知识和数形结合能力仔细分析即可解.
①由y=ax2+bx+c与X轴的交点坐标为(-2,0)得:
a×(-2)2+b×(-2 )+c=0,即4a-2b+c=0,
所以正确;
②由图象开口向下知a<0,
由y=ax2+bx+c与X轴的另一个交点坐标为(x1,0 ),且1<x1<2,
则该抛物线的对称轴为x=![]() =
=![]() ,即
,即![]() <1,
<1,
由a<0,两边都乘以a得:b>a,
∵a<0,对称轴x=-![]() <0,
<0,
∴b<0,
∴a<b<0.故正确;
③由一元二次方程根与系数的关系知x1x2=![]() ,结合a<0得2a+c>0,所以结论正确,
,结合a<0得2a+c>0,所以结论正确,
④由4a-2b+c=0得2ab=![]() ,而0<c<2,
,而0<c<2,
∴1<![]() ,
,
∴-1<2a-b<0∴2a-b+1>0,所以结论正确.
故正确结论的个数是4个.
故选D.


科目:初中数学 来源: 题型:
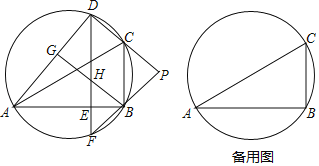
【题目】如图,D是△ABC外接圆上的动点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:BG∥CD;
(2)设△ABC外接圆的圆心为O,若AB=![]() DH,∠OHD=80°,求∠BDE的大小.
DH,∠OHD=80°,求∠BDE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
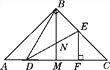
【题目】如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边上的中线,点D,E分别在边AC和BC上,DB=DE,DE与BM相交于点N,EF⊥AC于点F,以下结论:
①∠DBM=∠CDE;②S△BDE<S四边形BMFE;③CD·EN=BN·BD;④AC=2DF.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
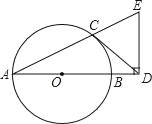
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AO![]() OM,OA=8,点B为射线OM上的一个动点,分别以OB、AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度是 ( )
OM,OA=8,点B为射线OM上的一个动点,分别以OB、AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度是 ( )

A. 3.6 B. 4 C. 4.8 D. PB的长度随B点的运动而变化
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
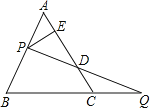
【题目】如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com