
 如图,等腰直角三角形ABD,点C是直角边AD上的动点,连接CB.现在将点C绕点A逆时针方向旋转90°得点E,再将点C绕点B顺时针方向旋转90°得点F.如果AD=BD=
如图,等腰直角三角形ABD,点C是直角边AD上的动点,连接CB.现在将点C绕点A逆时针方向旋转90°得点E,再将点C绕点B顺时针方向旋转90°得点F.如果AD=BD= ,那么S△AED+S△BFD-S△ABC=________.(其中S△AED表示△AED的面积)
,那么S△AED+S△BFD-S△ABC=________.(其中S△AED表示△AED的面积) ,由勾股定理,得AB=2,设AC=x,则AE=AM=CM=
,由勾股定理,得AB=2,设AC=x,则AE=AM=CM= x,由此可分别表示S△AED和S△ABC,利用S△BFD=
x,由此可分别表示S△AED和S△ABC,利用S△BFD= BF×DN,根据∠NDB+∠DBN=90°,∠DBN+∠CBD=90°,可证∠NDB=∠CBD,可证△BDN∽△CBD,利用相似比将BF×DN=DN×BC进行转化,继而可求得S△AED+S△BFD-S△ABC的值.
BF×DN,根据∠NDB+∠DBN=90°,∠DBN+∠CBD=90°,可证∠NDB=∠CBD,可证△BDN∽△CBD,利用相似比将BF×DN=DN×BC进行转化,继而可求得S△AED+S△BFD-S△ABC的值. 解:作CM⊥AB,DN⊥BF垂足分别为M,N,
解:作CM⊥AB,DN⊥BF垂足分别为M,N, x,
x, ,
, =2,
=2, ×AE×AD=
×AE×AD= x,S△ABC=
x,S△ABC= ×AB×CM=
×AB×CM= x,
x, ×BF×DN=
×BF×DN= ×DN×BC=1,
×DN×BC=1, x+1-
x+1- x=1.
x=1.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
 如图,等腰直角三角形ABC绕C点按顺时针旋转到△A1B1C1的位置(A、C、B1在同一直线上),∠B=90°,如果AB=1,那么AC运动到A1C1所经过的图形的面积是
如图,等腰直角三角形ABC绕C点按顺时针旋转到△A1B1C1的位置(A、C、B1在同一直线上),∠B=90°,如果AB=1,那么AC运动到A1C1所经过的图形的面积是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰直角三角形ABC的腰长与正方形DEFG的边长相符,且边AC与DE在同一直线l上,△ABC从如图所示的起始位置(A、E重合),沿直线l水平向右平移,直至C、D重合为止.设△ABC与正方形DEFG重叠部分的面积为y,平移的距离为x,则y与x之间的函数关系大致是( )
如图,等腰直角三角形ABC的腰长与正方形DEFG的边长相符,且边AC与DE在同一直线l上,△ABC从如图所示的起始位置(A、E重合),沿直线l水平向右平移,直至C、D重合为止.设△ABC与正方形DEFG重叠部分的面积为y,平移的距离为x,则y与x之间的函数关系大致是( )A、 | B、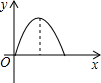 | C、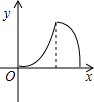 | D、 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M.
如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G.
如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰直角三角形AEF的顶点E在等腰直角三角形ABC的边BC上.AB的延长线交EF于D点,其中∠AEF=∠ABC=90°.
如图,等腰直角三角形AEF的顶点E在等腰直角三角形ABC的边BC上.AB的延长线交EF于D点,其中∠AEF=∠ABC=90°.| AD |
| AE |
| ||
| AC |
| DB |
| DA |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com