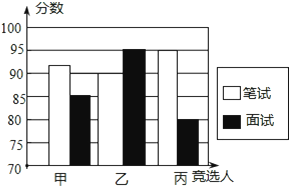
【题目】某初中学校欲向高一级学校推荐一名学生，根据规定的推荐程序：首先由本年级200名学生民主投票，每人只能推荐一人（不设弃权票），选出了票数最多的甲、乙、丙三人．投票结果统计如图一：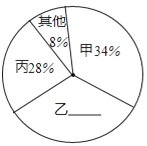

图一
其次，对三名候选人进行了笔试和面试两项测试．各项成绩如下表所示：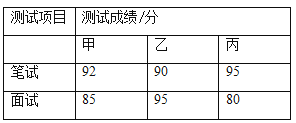

图二是某同学根据上表绘制的一个不完全的条形图．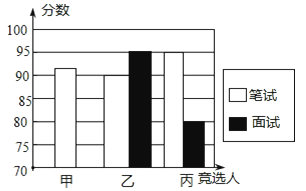

图二
请你根据以上信息解答下列问题：
（1）补全图一和图二；
（2）请计算每名候选人的得票数；
（3）若每名候选人得一票记1分，投票、笔试、面试三项得分按照2：5：3的比确定，计算三名候选人的平均成绩，成绩高的将被录取，应该录取谁？

参考答案：

【答案】
（1）

解答：解：

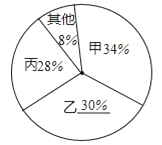
图一 图二


（2）

解答：根据题意得：甲的票数是：200×34％＝68（票），乙的票数是：200×30％＝60（票），丙的票数是：200×28％＝56（票）．

所以甲的票数是68票，乙的票数是60票，丙的票数是56票.


（3）

解答：应该录取丙.根据题意得：甲的平均成绩： ，乙的平均成绩： ，丙的平均成绩： ，∵丙的平均成绩最高，∴应该录取丙．


【解析】（1）由图1可看出，乙的得票所占的百分比为1减去“丙＋甲＋其他”的百分比；（2）由题意可分别求得三人的得票数，甲的得票数200×34％，乙的得票数200×30％，丙的得票数200×28％；（3）由题意可分别求得三人的得分，比较得出结论．
【考点精析】解答此题的关键在于理解扇形统计图的相关知识，掌握能清楚地表示出各部分在总体中所占的百分比．但是不能清楚地表示出每个项目的具体数目以及事物的变化情况，以及对条形统计图的理解，了解能清楚地表示出每个项目的具体数目，但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况．

关闭