
分析 (1)设每个房间每天的定价增加x元,利用当每个房间每天的定价增加10元时,就会有一间房空闲进而得出y与x之间的函数关系式;
(2)设每个房间每天的定价增加x元,宾馆所得利润为W,利用租房利润减去各种费用,可得利润函数关系式;
(3)利用公式法直接求出二次函数最值即可.
解答 解:(1)设每个房间每天的定价增加x元,
则一天订住的房间数y与x之间的函数关系式为:y=50-$\frac{x}{10}$;
(2)设每个房间每天的定价增加x元,宾馆所得利润为:
w=(180+x-20)(50-$\frac{x}{10}$),
即w=-$\frac{1}{10}$x2+34x+8000;
(3)由题意可得:0≤x≤500,且x是10的倍数.
当x=-$\frac{b}{2a}$=170时,
∴房价定为180+170=350时,宾馆利润最大.
∴y最大=10890(元).
答:房价定为350元,宾馆利润最大,一天的最大利润为10890元.
点评 本题考查了二次函数的应用,要求同学们仔细审题,将实际问题转化为数学模型,注意公式法求二次函数最值的应用.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 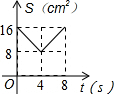 | B. | 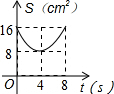 | C. | 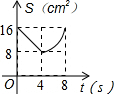 | D. | 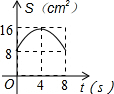 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运往甲地(单位:吨) | 运往乙地(单位:吨) | |
| A | x | 14-x |
| B | 15-x | x-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
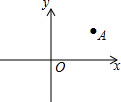 如图,已知点A(2,3),将点A绕原点O顺时针旋转90°到A′,则点A′的坐标为( )
如图,已知点A(2,3),将点A绕原点O顺时针旋转90°到A′,则点A′的坐标为( )| A. | (-2,3) | B. | (-3,2) | C. | (2,-3) | D. | (3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com