

分析 (1)利用三角形的内角和定理表示出∠AOD与∠BOC,再根据对顶角相等可得∠AOD=∠BOC,然后整理即可得解;
(2)根据(1)的关系式求出∠OCB-∠OAD,再根据角平分线的定义求出∠DAM-∠PCM,然后利用“8字形”的关系式列式整理即可得解;
(3)根据“8字形”用∠B、∠D表示出∠OCB-∠OAD,再用∠D、∠P表示出∠DAM-∠PCM,然后根据角平分线的定义可得∠DAM-∠PCM=$\frac{1}{2}$(∠OCB-∠OAD),然后整理即可得证.
解答  解:(1)在△AOD中,∠AOD=180°-∠A-∠D,
解:(1)在△AOD中,∠AOD=180°-∠A-∠D,
在△BOC中,∠BOC=180°-∠B-∠C,
∵∠AOD=∠BOC(对顶角相等),
∴180°-∠A-∠D=180°-∠B-∠C,
∴∠A+∠D=∠B+∠C,
故答案为;∠A+∠D=∠B+∠C;
(2)∵∠D=40°,∠B=36°,
∴∠OAD+40°=∠OCB+36°,
∴∠OCB-∠OAD=4°,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=$\frac{1}{2}$∠OAD,∠PCM=$\frac{1}{2}$∠OCB,
又∵∠DAM+∠D=∠PCM+∠P,
∴∠P=∠DAM+∠D-∠PCM=$\frac{1}{2}$(∠OAD-∠OCB)+∠D=$\frac{1}{2}$×(-4°)+40°=38°,
故答案为:38°;
(3)根据“8字形”数量关系,∠OAD+∠D=∠OCB+∠B,∠DAM+∠D=∠PCM+∠P,
所以,∠OCB-∠OAD=∠D-∠B,∠PCM-∠DAM=∠D-∠P,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=$\frac{1}{2}$∠OAD,∠PCM=$\frac{1}{2}$∠OCB,
∴$\frac{1}{2}$(∠D-∠B)=∠D-∠P,
整理得,2∠P=∠B+∠D.
点评 本题考查了三角形内角和定理,角平分线的定义,多边形的内角和定理,对顶角相等的性质,整体思想的利用是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
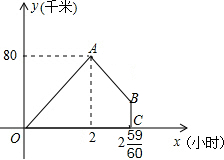 甲地宏达物流公司的快递车和货车同时从甲地出发,以各自的速度沿快速通道向乙地匀速行驶,快递车到达乙地后,卸完物资并另装货物共用了45分钟,然后按原路以另一速度返回,直至与货车相遇,已知货车行驶速度为60km/h,两车间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示
甲地宏达物流公司的快递车和货车同时从甲地出发,以各自的速度沿快速通道向乙地匀速行驶,快递车到达乙地后,卸完物资并另装货物共用了45分钟,然后按原路以另一速度返回,直至与货车相遇,已知货车行驶速度为60km/h,两车间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲同学:平均数为2,中位数为2 | B. | 乙同学:中位数是2,唯一的众数为2 | ||
| C. | 丙同学:平均数是2,标准差为2 | D. | 丁同学:平均数为2,唯一的众数为2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com