
| A. | 甲同学:平均数为2,中位数为2 | B. | 乙同学:中位数是2,唯一的众数为2 | ||
| C. | 丙同学:平均数是2,标准差为2 | D. | 丁同学:平均数为2,唯一的众数为2 |
分析 根据平均数、中位数、众数、标准差的意义,分别分析各选项,举出反例利用排除法即可求解.
解答 解:A、由于中位数为2,那么5门学科的名次为1,1,2,x,y或者1,2,2,x,y(2≤x≤y),由平均数为2得出x+y=6或5,当x=2时,y=4(不合题意)或3,故本选项错误;
B、由于中位数为2,那么5门学科的名次为1,1,2,x,y,或者1,2,2,x,y,(2≤x≤y),由唯一的众数为2,那么第二种情况1,2,2,x,y,当x=4,y=5时不合题意,故本选项错误;
C、由标准差为2,得出方差为4,设5门学科的名次为x1,x2,x3,x4,x5,那么$\frac{1}{5}$[(x1-2)2+(x2-2)2+…+(x5-2)2]=4,整理得x12+x22+…+x52=40,那么这五个数可以是1,1,2,3,5,不合题意,故本选项错误;
D、由唯一的众数为2,那么5门学科的名次为2,2,x,y,z,由平均数为2,得出x+y+z=6,x,y,z可以是1,1,4或1,2,3,而1,1,4与唯一的众数为2不符,所以x,y,z是1,2,3,符合题意,故本选项正确.
故选D.
点评 本题考查了平均数、中位数、众数、标准差的意义,平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.一组数据中出现次数最多的数据叫做众数.样本方差的算术平方根表示样本的标准差,它也描述了数据对平均数的离散程度.本题有一定难度,透彻理解定义是解题的关键.


科目:初中数学 来源: 题型:选择题
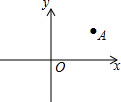 如图,已知点A(2,3),将点A绕原点O顺时针旋转90°到A′,则点A′的坐标为( )
如图,已知点A(2,3),将点A绕原点O顺时针旋转90°到A′,则点A′的坐标为( )| A. | (-2,3) | B. | (-3,2) | C. | (2,-3) | D. | (3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
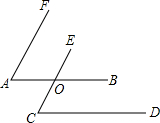 如图,∠FAB与∠ECD都是锐角,其中AB∥CD,AF∥CE,射线AB与CE相交于点O,若∠FAB=60°,则∠ECD的度数是( )
如图,∠FAB与∠ECD都是锐角,其中AB∥CD,AF∥CE,射线AB与CE相交于点O,若∠FAB=60°,则∠ECD的度数是( )| A. | 30° | B. | 60° | C. | 80° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\underset{\frac{1}{2}}{\;}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 快、慢两车分别从相距480km的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图象,结合图象解答下列问题:
快、慢两车分别从相距480km的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图象,结合图象解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com