
【题目】如图,AD是△ABC的中线,tanB=![]() , cosC=
, cosC=![]() , AC=
, AC=![]() . 求:
. 求:
(1)BC的长;
(2)sin∠ADC的值.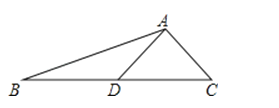
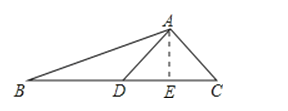
【答案】解:(1)过点A作AE⊥BC于点E,
∵cosC=![]() ,
,
∴∠C=45°,
在Rt△ACE中,CE=ACcosC=1,
∴AE=CE=1,
在Rt△ABE中,tanB=![]() ,即
,即![]() =
=![]() ,
,
∴BE=3AE=3,
∴BC=BE+CE=4;
(2)∵AD是△ABC的中线,
∴CD=![]() BC=2,
BC=2,
∴DE=CD﹣CE=1,
∵AE⊥BC,DE=AE,
∴∠ADC=45°,
∴sin∠ADC=![]() .
.
【解析】(1)过点A作AE⊥BC于点E,根据cosC=![]() , 求出∠C=45°,求出AE=CE=1,根据tanB=
, 求出∠C=45°,求出AE=CE=1,根据tanB=![]() , 求出BE的长即可;
, 求出BE的长即可;
(2)根据AD是△ABC的中线,求出BD的长,得到DE的长,得到答案.
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】A,B两点在数轴上的位置如图所示,O为原点,现A,B两点分别以1个单位长度/秒的速度同时向左运动。
(1)几秒后,原点恰好在A,B两点正中间?
(2)几秒后,恰好有OA:OB=1:2.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门BC打开的宽度为2米,以下哪辆车可以通过?( )
(栏杆宽度,汽车反光镜忽略不计)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)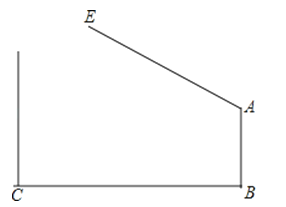
A.宝马Z4(4200mm×1800mm×1360mm)
B.奇瑞QQ(4000mm×1600mm×1520mm)
C.大众朗逸(4600mm×1700mm×1400mm)
D.奥迪A4(4700mm×1800mm×1400mm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…依此类推,则a2015的值为( )
A. ﹣2015 B. ﹣2014 C. ﹣1007 D. ﹣1008
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道不等式的两边加(或减)同一个数(或式子),不等号的方向不变.不等式组是否也具有类似的性质呢?请解答下列问题.
(1)完成下列填空:
已知 | 用“<”或“>”填空 |
| 5+2_____3+1 |
| ﹣3﹣1_____﹣5﹣2 |
| 1﹣2_____4+1 |
(2)一般地,如果![]() 那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
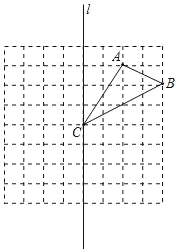
【题目】在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点).
(1)△ABC的面积为 ;
(2)在直线l上找一点P,使点P到边AB、BC的距离相等.
(3)画出△ABC关于直线l对称的图形△A1B1C1;再将△A1B1C1向下平移4个单位,画出平移后得到的△A2B2C2.
(4)结合轴对称变换和平移变换的有关性质,两个对应三角形△ABC和△A2B2C2的对应点所具有的性质是( ).
A.对应点连线与对称轴垂直 B.对应点连线被对称轴平分或与对称轴重合
C.对应点连线被对称轴垂直平分 D.对应点连线互相平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=44°,∠BAD=28°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC= 度;
(2)求∠EDF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论: ①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),
其中正确结论的个数是( )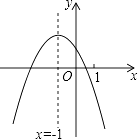
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
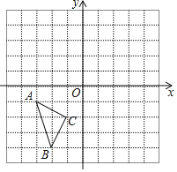
【题目】在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(–3,–1).
(1)将△ABC先沿x轴向右平移3个单位,再沿y轴向上平移2个单位得到△A1B1C1,画出△A1B1C1,并写出点B1坐标.
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点C2的坐标.
(3)求出△A2B2C2的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com