
【题目】如图,![]() 中,
中,![]() ,高
,高![]() 、
、![]() 相交于点
相交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,则图中全等的直角三角形共有( )
,则图中全等的直角三角形共有( )
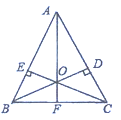
A.4对B.5对C.![]() 对D.7对
对D.7对
【答案】C
【解析】
首先根据等腰三角形得到∠ABC=∠ACB,证明△BCE≌△CBD,得到BE=CD,可证△OBE≌△OCD,同时得到AE=AD,再证明△ABD≌△ACF,得到EO=DO,证明△OAE≌△OAD得到∠BAF=∠CAF ,证得△ABF≌△ACF,△OBF≌△OCF,故可求解.
∵![]() ,∴∠ABC=∠ACB
,∴∠ABC=∠ACB
∵高![]() 、
、![]() 相交于点
相交于点![]() ,∴∠BEC=∠CDB,又BC=CB,
,∴∠BEC=∠CDB,又BC=CB,
∴△BCE≌△CBD(AAS),
∴BE=CD,∴AE=AD
∴△ABD≌△ACF(SAS),
又∠BOE=∠COD,∴△OBE≌△OCD(AAS),∴EO=DO
∴△OAE≌△OAD(SSS)
∴∠BAF=∠CAF ,
∴△ABF≌△ACF(SAS),
∴BF=CF
∴△OBF≌△OCF(SSS)
故有6对全等的直角三角形
故选C


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2,对角线AC、BD交于点O,∠AOD=120°,E为BD上任意点,P为AE中点,则PO+PB的最小值为 ( )

A.![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
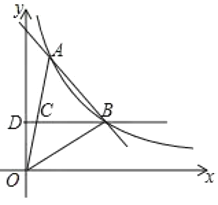
【题目】如图,一次函数y=ax+b与反比例函数y=![]() (x>0)的图像在第一象限交于A、B两点,点B坐标为(4,2),连接OA、OB,过点B作BD⊥y轴,垂足为D,交OA于点C,且OC=CA.
(x>0)的图像在第一象限交于A、B两点,点B坐标为(4,2),连接OA、OB,过点B作BD⊥y轴,垂足为D,交OA于点C,且OC=CA.
(1)求反比例函数和一次函数的表达式;
(2)根据图像直接说出不等式ax+b-![]() <0的解集为______;
<0的解集为______;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:请你参与下面探究过程,完成所提出的问题.
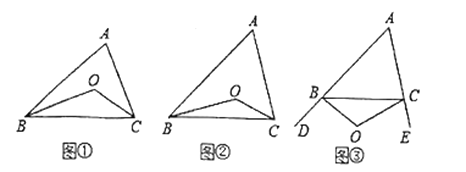
(I)问题引入:
如图①,在![]() 中,点
中,点![]() 是
是![]() 和
和![]() 平分线的交点,若
平分线的交点,若![]() ,则
,则![]()
![]() 度;若
度;若![]() ,则
,则![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(II)类比探究:
如图②,在![]() 中,
中,![]() ,
,![]() ,
,![]() .试探究:
.试探究:![]() 与
与![]() 的数量关系(用含
的数量关系(用含![]() 的代数式表示),并说明理由.
的代数式表示),并说明理由.
(III)知识拓展:
如图③,![]() 、
、![]() 分别是
分别是![]() 的外角
的外角![]() ,
,![]() 的
的![]() 等分线,它们的交于点
等分线,它们的交于点![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数(用含
的度数(用含![]() 、
、![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进西装30件,衬衫45件,共用了39000元,其中西装的单价是衬衫的5倍。
(1)求西装和衬衫的单价各为多少元?
(2)商场仍需要购买上面的两种产品55件(每种产品的单价不变),采购部预算共支出32000元,财会算了一下,说:“如果你用这些钱共买这两种产品,那么账肯定算错了”请你用学过的方程知识解释财会为什么会这样说?
查看答案和解析>>
科目:初中数学 来源: 题型:
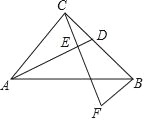
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F.
求证:AC=2BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成如下不完整的条形图和扇形图.

请结合以上信息解答下列问题:
(1)m= ;
(2)请补全上面的条形统计图;
(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为 ;
(4)已知该校共有1200名学生,请你估计该校约有 名学生最喜爱足球活动.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,![]() 的顶点坐标为:
的顶点坐标为:![]() ,
,![]() ,
,![]() .
.

(1)将![]() 向左平移2个单位长度,再向上平移1个单位长度,得
向左平移2个单位长度,再向上平移1个单位长度,得![]() .画出
.画出![]() 并写出
并写出![]() 的顶点坐标;
的顶点坐标;
(2)请判断![]() 的形状并求它的面积.
的形状并求它的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com