
【题目】在△ABC中,AC=6![]() ,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为
,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为![]() ,并且CD⊥AC,则BC的长为________.
,并且CD⊥AC,则BC的长为________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
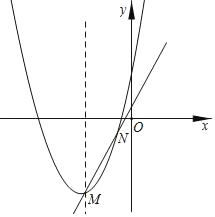
【题目】如图,已知抛物线y=x2+px+q的对称轴为直线x=﹣2,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(﹣1,﹣1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( ).
A. (0,﹣2) B. (0,﹣![]() ) C. (0,﹣
) C. (0,﹣![]() ) D. (0,﹣
) D. (0,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛一枚均匀硬币正面朝上的概率为![]() ,下列说法错误的是
,下列说法错误的是![]()
![]()
A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次都可能正面朝上
C. 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=150°,AC=4,tanB=![]() .
.
(1)求BC的长;
(2)利用此图形求tan15°的值(精确到0.1,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈2.2).
≈2.2).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
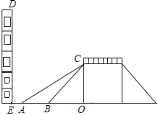
【题目】如图是某一过街天桥的示意图,天桥高![]() 为
为![]() 米,坡道倾斜角
米,坡道倾斜角![]() 为
为![]() ,在距
,在距![]() 点
点![]() 米处有一建筑物
米处有一建筑物![]() .为方便行人上下天桥,市政部门决定减少坡道的倾斜角,但要求建筑物与新坡角
.为方便行人上下天桥,市政部门决定减少坡道的倾斜角,但要求建筑物与新坡角![]() 处之间地面要留出不少于
处之间地面要留出不少于![]() 米宽的人行道.
米宽的人行道.
![]() 若将倾斜角改建为
若将倾斜角改建为![]() (即
(即![]() ),则建筑物
),则建筑物![]() 是否要拆除?(
是否要拆除?(![]() )
)
![]() 若不拆除建筑物
若不拆除建筑物![]() ,则倾斜角最小能改到多少度(精确到
,则倾斜角最小能改到多少度(精确到![]() )?
)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们规定:当x取任意一个值时,x对应的函数值分别为y1和y2,若y1≠y2,取y1和y2中较小值为M;若y1=y2,记M=y1=y2.①当x>2时,M=y2;②当x<0时,M随x的增大而增大;③使得M大于4的x的值不存在;④若M=2,则x=1.上述结论正确的是_____(填写所有正确结论的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com