
【题目】如图,在正方形![]() 中,边长为2的等边三角形
中,边长为2的等边三角形![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() 和
和![]() 上,则正方形
上,则正方形![]() 的面积等于_________.
的面积等于_________.

【答案】![]()
【解析】
首先根据四边形![]() 是正方形得出AB=AD,∠B=∠D=90°,根据△AEF是等边三角形得出AE=AF,最后根据HL即可证明△ABE≌△ADF;根据全等的性质:CE=CF,∠C=90°,从而得出△ECF是等腰直角三角形,再根据勾股定理得出EC的值,设
是正方形得出AB=AD,∠B=∠D=90°,根据△AEF是等边三角形得出AE=AF,最后根据HL即可证明△ABE≌△ADF;根据全等的性质:CE=CF,∠C=90°,从而得出△ECF是等腰直角三角形,再根据勾股定理得出EC的值,设![]() ,则
,则![]() ,在Rt△ABE中,
,在Rt△ABE中,![]() ,求出
,求出![]() 的值,即可得出正方形
的值,即可得出正方形![]() 的边长,最后求出正方形
的边长,最后求出正方形![]() 的面积.
的面积.
解:∵四边形![]() 是正方形,∴AB=AD,∠B=∠D=90°,
是正方形,∴AB=AD,∠B=∠D=90°,
∵△AEF是等边三角形,∴AE=AF,
在Rt△ABE和Rt△ADF中,
![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴CE=CF,∠C=90°,
即△ECF是等腰直角三角形,
由勾股定理得![]() ,
,
∴![]() ,
,
在Rt△ABE中,![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
∴![]() ,
,
∴![]() ,
,
故答案为![]() .
.


科目:初中数学 来源: 题型:
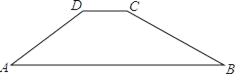
【题目】如图所示,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,斜坡AD=8m,斜坡BC的坡度i=1:3,B,C间的水平距离为12m,则斜坡AD的坡角∠A=_____,坝底宽AB=______m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图,若双曲线![]() (k>0)与它的其中一条对称轴y=x相交于两点A,B,则线段AB的长称为双曲线
(k>0)与它的其中一条对称轴y=x相交于两点A,B,则线段AB的长称为双曲线![]() (k>0)的对径.
(k>0)的对径.

(1)求双曲线![]() 的对径;
的对径;
(2)若某双曲线![]() (k>0)的对径是
(k>0)的对径是![]() .求k的值.
.求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=6![]() ,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为
,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为![]() ,并且CD⊥AC,则BC的长为________.
,并且CD⊥AC,则BC的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,以点
的中点,以点![]() 为圆心、
为圆心、![]() 长为半径作圆,恰好点
长为半径作圆,恰好点![]() 在
在![]() 上,连接
上,连接![]() ,若
,若![]() ,下列说法中不正确的是( )
,下列说法中不正确的是( )
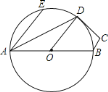
A. D是劣弧BE的中点 B. CD是⊙O的切线 C. AE//OD D. ∠DOB=∠EAD
查看答案和解析>>
科目:初中数学 来源: 题型:
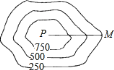
【题目】如图,测量队为了测量某地区山顶![]() 的海拔高度,选
的海拔高度,选![]() 点作为观测点,从
点作为观测点,从![]() 点测量山顶
点测量山顶![]() 的仰角(视线在水平线上方,与水平线所夹的角)为
的仰角(视线在水平线上方,与水平线所夹的角)为![]() ,在比例尺为
,在比例尺为![]() 的该地区等高线地形图上,量得这两点的图上距离为
的该地区等高线地形图上,量得这两点的图上距离为![]() 厘米,则山顶
厘米,则山顶![]() 的海拔高度为( )
的海拔高度为( )
A. ![]() 米 B.
米 B. ![]() 米 C.
米 C. ![]() 米 D.
米 D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的周长是20cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为68cm2,那么矩形ABCD的面积是( )
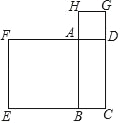
A. 9cm2 B. 16cm2 C. 21cm2 D. 24cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求证:AD⊥EF;
(2)求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com