
【题目】如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求证:AD⊥EF;
(2)求CG的长.
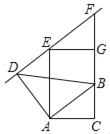
【答案】(1)证明见解析;(2)CG= 12.5.
【解析】
(1)由平移的性质可知:AB∥DF,再利用平行线的性质即可证明;
(2)先判断出∠ADE=∠ACB,进而得出△ADE∽△ACB,得出比例式求出AE,即可得出结论.
(1)∵线段AD是由线段AB绕点A按逆时针方向旋转90°得到,
∴∠DAB=90°,
∵△EFG是△ABC沿CB方向平移得到,
∴AB∥EF,
∴∠ADF+∠DAB=180°,
∴∠ADF=90°,
∴AD⊥EF;
(2)由平移的性质得,AE∥CG,AB∥EF,
∴∠DEA=∠DFC=∠ABC,∠ADE+∠DAB=180°,
∵∠DAB=90°,
∴∠ADE=90°,
∵∠ACB=90°,
∴∠ADE=∠ACB,
∴△ADE∽△ACB,
∴![]() =
=![]() ,
,
∵AC=8,AB=AD=10,
∴AE=12.5,
由平移的性质得,CG=AE=12.5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
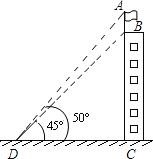
【题目】测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
(1)若已知CD=20米,求建筑物BC的高度;
(2)若已知旗杆的高度AB=5米,求建筑物BC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
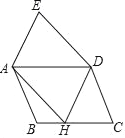
【题目】如图,将平行四边形ABCD绕点D旋转,点C落在BC上的点H处,点B恰好落在点A处,得平行四边形DHAE,若BH=2,CH=3,则DC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
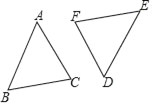
【题目】如图,△ABC和△DEF关于点O成中心对称.
(1)作出它们的对称中心O,并简要说明作法;
(2)若AB=6,AC=5,BC=4,求△DEF的周长;
(3)连接AF,CD,试判断四边形ACDF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶MN上晒太阳.
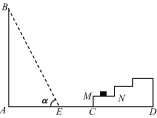
(1)求楼房的高度约为多少米?(结果精确到0.1米)
(2)过了一会儿,当α=45°时,小猫还能不能晒到太阳?请说明理由.(参考数据:![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
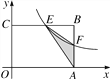
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com