
【题目】如图所示,一幢楼房AB背后有台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶MN上晒太阳.
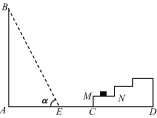
(1)求楼房的高度约为多少米?(结果精确到0.1米)
(2)过了一会儿,当α=45°时,小猫还能不能晒到太阳?请说明理由.(参考数据:![]() ≈1.732)
≈1.732)
【答案】(1)楼房的高度约为17.3米;(2)当α=45°时,小猫还能晒到太阳.
【解析】
(1)在Rt△ABE中,由tan 60°=![]() ,即可求出AB的长;
,即可求出AB的长;
(2)假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.由∠BFA=45°,可得AF=AB=17.3米,那么CF=AF-AC=0.1米,CH=CF=0.1米,所以大楼的影子落在台阶MC这个侧面上,故小猫仍可以晒到太阳.
解:(1)当α=60°时,在Rt△ABE中,
∵tan 60°=![]() ,
,
∴AB=10·tan 60°=10![]() ≈10×1.73=17.3米.
≈10×1.73=17.3米.
∴楼房的高度约为17.3米.
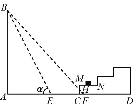
(2)当α=45°时,小猫还能晒到太阳.
理由:假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为F,与MC的交点为H.
∵∠BFA=45°,∴tan 45°=![]() =1,
=1,
此时的影长AF=AB=17.3米,
∴CF=AF-AC=0.1米,∴CH=CF=0.1米,
∴大楼的影子落在台阶MC这个侧面上,
∴小猫还能晒到太阳.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
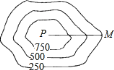
【题目】如图,测量队为了测量某地区山顶![]() 的海拔高度,选
的海拔高度,选![]() 点作为观测点,从
点作为观测点,从![]() 点测量山顶
点测量山顶![]() 的仰角(视线在水平线上方,与水平线所夹的角)为
的仰角(视线在水平线上方,与水平线所夹的角)为![]() ,在比例尺为
,在比例尺为![]() 的该地区等高线地形图上,量得这两点的图上距离为
的该地区等高线地形图上,量得这两点的图上距离为![]() 厘米,则山顶
厘米,则山顶![]() 的海拔高度为( )
的海拔高度为( )
A. ![]() 米 B.
米 B. ![]() 米 C.
米 C. ![]() 米 D.
米 D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
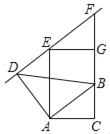
【题目】如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求证:AD⊥EF;
(2)求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
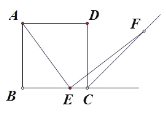
【题目】如图,四边形 ABCD 是正方形,点 E是 BC边上任意一点, AEF 90°,且EF 交正方形外角的平分线 CF 于点 F.求证:AE=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
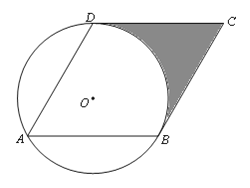
【题目】已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列说法不正确的是( )
(k≠0),下列说法不正确的是( )
A. 它的图象分布在第一、三象限 B. 点(k,k)在它的图象上
C. 它的图象关于原点对称 D. 在每个象限内y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某空调厂的装配车间计划组装9000台空调.
(1)从组装空调开始,每天组装的台数m(单位:台/天)与生产时间t(单位:天)之间有怎样的函数关系?
(2)原计划用2个月时间(每月以30天计算)完成,由于气温提前升高,厂家决定这批空调提前10天上市,那么原装配车间每天至少要组装多少台空调?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.

(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com