
【题目】在平面直角坐标系中,我们定义直线![]() 为抛物线
为抛物线![]() (a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”,已知抛物线
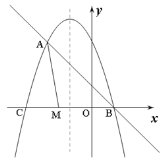
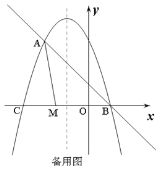
(a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”,已知抛物线![]() 与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,点A的坐标为 ,点B的坐标为 ;
(2)如图,点M为线段BC上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)在该抛物线的“梦想直线”上,是否存在点P,使△ACP为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;
;![]() ;
;![]() ;(2)(0,
;(2)(0,![]() );(3)(0,1),(
);(3)(0,1),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).
【解析】
(1)由梦想直线的定义可求得其解析式,联立梦想直线与抛物线解析式可求得![]() 、
、![]() 的坐标;
的坐标;
(2)当![]() 点在
点在![]() 轴上时,过
轴上时,过![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() ,
,![]() ,
,![]() ,利用勾股定理,可以得出AC的长,设N点坐标为:(0,y),根据翻转,可得
,利用勾股定理,可以得出AC的长,设N点坐标为:(0,y),根据翻转,可得![]() ,结合
,结合![]() 点坐标,利用勾股定理,可求得
点坐标,利用勾股定理,可求得![]() 点坐标;
点坐标;
(3)分3种情况:当![]() 时,当
时,当![]() 时,当
时,当![]() 时,分别结合题目的已知条件进行讨论,即可求出P点坐标.
时,分别结合题目的已知条件进行讨论,即可求出P点坐标.
解:(1)![]() 抛物线
抛物线![]() ,
,
![]() 其梦想直线的解析式为
其梦想直线的解析式为![]() ,
,
联立梦想直线与抛物线解析式可得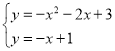 ,解得
,解得![]() 或
或![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
故答案为:![]() ;
;![]() ;
;![]() ;
;
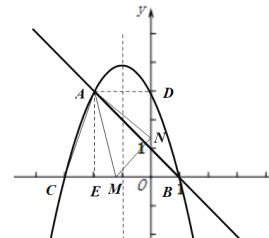
(2)当点![]() 在
在![]() 轴上时,
轴上时,![]() 为梦想三角形,
为梦想三角形,
如图,过![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
设N点坐标为:(0,y)(![]() ),则
),则![]() ,
,
∵将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,
则有![]() ,即:
,即:![]() ,
,
解之得:![]() ,
,
∴N的坐标为:(0,![]() );
);
(3)在该抛物线的“梦想直线”上,存在点P,使△ACP为等腰三角形,
∵抛物线![]() 中,当
中,当![]() 时,
时,![]() ,
,![]() ,
,
∴C的坐标为:(-3,0);
设P点坐标为:(x,-x+1)
①如图示,
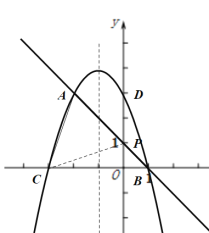
当![]() 时,即有
时,即有 ![]()
解之得:![]() ,
,![]() ,
,
∴P点坐标为:(0,1),(-2,3)(此点为A点,不合题意,舍去)
②如图示,
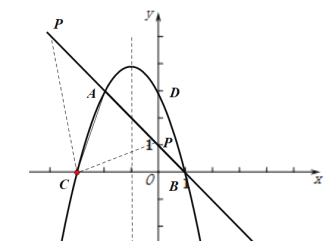
当![]() 时,即有
时,即有 ![]()
解之得:![]() ,
,![]() ,
,
∴![]() ,
,![]()
∴P点坐标为:(![]() ,
,![]() ),(
),(![]() ,
,![]() );
);
③如图示,
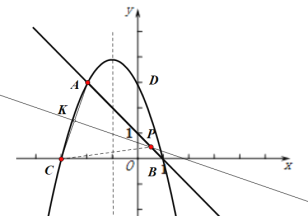
当![]() 时,作AC的垂直平分线KP,KP交AC于点K,
时,作AC的垂直平分线KP,KP交AC于点K,
∴K的坐标为:(-2.5,1.5),
∵A的坐标为:(-2,3),C的坐标为:(-3,0),
∴![]() ,
,
∴![]() ,
,
∴![]() ,将(-2.5,1.5)代入,则
,将(-2.5,1.5)代入,则![]()
∴KP的解析式为:![]()
联立梦想直线与直线KP的解析式可得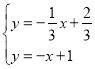 ,解得
,解得![]()
∴P点坐标为:(![]() ,
,![]() ),
),
综上所述,P点坐标为:(0,1),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() );
);


科目:初中数学 来源: 题型:
【题目】若整数a既使得关于x的分式方程![]() 有非负数解,又使得关于x的不等式x2-x+a+5≥0恒成立,则符合条件的所有a的个数为( )
有非负数解,又使得关于x的不等式x2-x+a+5≥0恒成立,则符合条件的所有a的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC的平分线AD与边BC的垂直平分线ED相交于点D,过点D作DF⊥AC交AC延长线于点F,若AB=8,AC=4,则CF的长为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.

(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
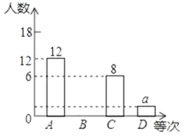
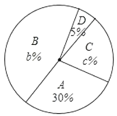
【题目】2020年,一场突然而来的新型冠状病毒肺炎疫情阻挡了学生们开学的脚步,多地学校进行了“战役在家,线上课堂”活动,保证学生离校不离学,为减少初中生被网络诈骗的案件,因此要求学生掌握防诈骗知识并进行网络测评.为了解某校学生的测试情况,从中随机抽取部分学生的成绩进行统计,并把测试成绩分为A.B.C.D四个等次,绘制成如图所示的不完整的统计图,请你依图解答下列问题:
(1)a= ,b= ,c= ;
(2)请将条形统计图补充完整,并计算表示C等次的扇形所对的圆心角的度数;
(3)学校决定从A等次的甲、乙、丙、丁四名学生中,随机选取两名学生参加全市中学生防网络诈骗知识竞赛,请用列表法或画树状图法,求甲、乙两名学生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
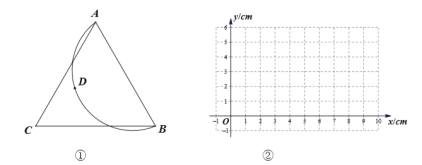
【题目】如图,点![]() 是
是![]() 上(除点
上(除点![]() 外)一点,以
外)一点,以![]() 为边作等边
为边作等边![]() ,与
,与![]() 交于两点.记
交于两点.记![]() 的长为
的长为![]() ,点
,点![]() 到
到![]() 的距离为
的距离为![]() ,点
,点![]() 到
到![]() 的距离为
的距离为![]() :
:
小腾根据学习函数的经验,对![]() ,
,![]() ,
,![]() 的长度之间的关系进行了探究.
的长度之间的关系进行了探究.
下面是小腾的探究过程,请补充完整:
(1)对于点![]() 在
在![]() 上的不同位置,画图、测量,得到了
上的不同位置,画图、测量,得到了![]() ,
,![]() ,
,![]() 的长度几组值,如下表:
的长度几组值,如下表:
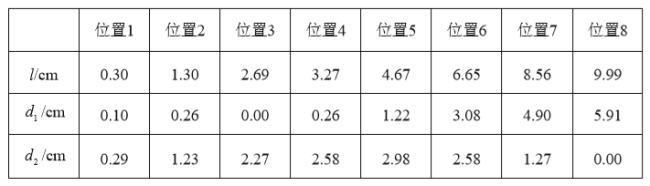
在![]() ,
,![]() ,
,![]() 的长度这三个量中,确定 是自变量, 和 都是这个自变量的函数;
的长度这三个量中,确定 是自变量, 和 都是这个自变量的函数;
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图像;
中,画出(1)中所确定的函数的图像;
(3)结合函数图像,解决问题:当点![]() 在
在![]() 平分线上时,
平分线上时,![]() 的长约为 cm.
的长约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )

A. 6![]() B. 10 C. 2
B. 10 C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
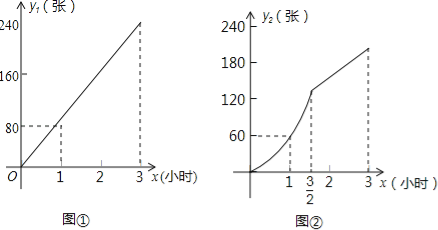
【题目】某市对火车站进行了大规模的改建,改建后的火车站除原有的普通售票窗口外,新增了自动打印车票的无人售票窗口.某日,从早8点开始到上午11点,每个普通售票窗口售出的车票数y1(张)与售票时间x(小时)的正比例函数关系满足图①中的图象,每个无人售票窗口售出的车票数y2(张)与售票时间x(小时)的函数关系满足图②中的图象.
(1)图②中图象的前半段(含端点)是以原点为顶点的抛物线的一部分,根据图中所给数据确定抛物线的表达式为 ,其中自变量x的取值范围是 ;
(2)若当天共开放5个无人售票窗口,截至上午9点,两种窗口共售出的车票数不少于1450张,则至少需要开放多少个普通售票窗口?
(3)上午10点时,每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同,试确定图②中图象的后半段一次函数的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com