
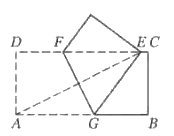
【题目】如图,已知在矩形纸片![]() 中,
中,![]() 将纸片折叠,使顶点
将纸片折叠,使顶点![]() 与边
与边![]() 的点
的点![]() 重合.若折痕
重合.若折痕![]() 分别与
分别与![]() 交于点
交于点![]() 的外接圆与直线
的外接圆与直线![]() 有唯一一个公共点,则折痕
有唯一一个公共点,则折痕![]() 的为______.
的为______.
【答案】![]()
【解析】
根据折叠的性质判断出AG=GE,∠AGF=∠EGF,再由CD∥AB得出∠EFG=∠AGF,从而判断出EF=AG,得出四边形AGEF是平行四边形,继而结合AG=GE,判定四边形AGEF是菱形;连接ON,得出ON是梯形ABCE的中位线,在RT△ADE中,利用勾股定理可解出x,继而可得出折痕FG的长度.
由折叠的性质可得,GA=GE,∠AGF=∠EGF,
∵DC∥AB,
∴∠EFG=∠AGF,
∴∠EFG=∠EGF,
∴EF=EG=AG,
∴四边形AGEF是平行四边形(EF∥AG,EF=AG),
又∵AG=GE,
∴四边形AGEF是菱形
令△AED的外接圆与直线![]() 有唯一一个公共点为N,连接ON,如图所示,
有唯一一个公共点为N,连接ON,如图所示,
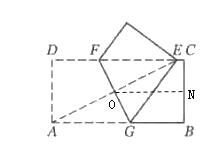
∵△AED是直角三角形,AE是斜边,点O是AE的中点,△AED的外接圆与BC相切于点N,
∴ON⊥BC,
∵点O是AE的中点,
∴ON是梯形ABCE的中位线,
设CE=x,则ED=2-x,2ON=CE+AB=x+2,
在Rt△AED中,AE=2OE=2ON=x+2,
AD2+DE2=AE2,
∴12+(2-x)2=(2+x)2,
得x=![]() ,
,
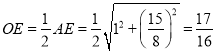 ,
,
∵△FEO∽△AED,
∴![]() ,
,
解得:FO=![]() ,
,
∴FG=2FO=![]() .
.
故答案为:![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】已知:有代数式①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .若从中随机抽取两个,用“=”连接.
.若从中随机抽取两个,用“=”连接.
(1)写出能得到的一元二次方程;
(2)从(1)中得到的一元二次方程中挑选一个进行解方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
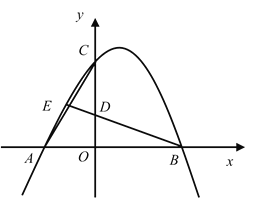
【题目】如图,已知抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() 、
、![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() .
.
(1)求抛物线![]() 的表达式;
的表达式;
(2)若抛物线![]() 与抛物线
与抛物线![]() 关于
关于![]() 轴对称,在抛物线
轴对称,在抛物线![]() 位于第二象限的部分上取一点
位于第二象限的部分上取一点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,是否存在这样的点
,是否存在这样的点![]() ,使得
,使得![]() 与
与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、B、C的坐标分别为(0,5)(0,2)(4,2),直线l的解析式为y = kx+5-4k(k > 0).
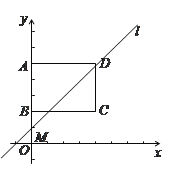
(1)当直线l经过点B时,求一次函数的解析式;
(2)通过计算说明:不论k为何值,直线l总经过点D;
(3)直线l与y轴交于点M,点N是线段DM上的一点, 且△NBD为等腰三角形,试探究:
①当函数y = kx+5-4k为正比例函数时,点N的个数有 个;
②点M在不同位置时,k的取值会相应变化,点N的个数情况可能会改变,请直接写出点N所有不同的个数情况以及相应的k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,其中a>0.
,其中a>0.
(1)若方程![]() 有两个实根
有两个实根![]() ,且方程
,且方程![]() 有两个相等的实根,求二次函数的解析式;
有两个相等的实根,求二次函数的解析式;
(2)若二次函数![]() 的图象与x轴交于
的图象与x轴交于![]() 两点,且当
两点,且当![]() 时,
时,![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
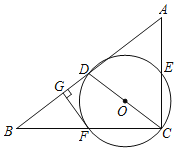
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,以CD为直径的⊙O分别交AC,BC于点E,F两点,过点F作FG⊥AB于点G.
(1)试判断FG与⊙O的位置关系,并说明理由.
(2)若AC=3,CD=2.5,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.
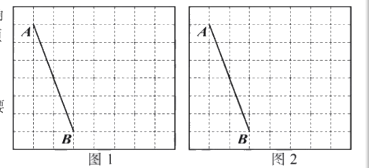
(1)在图1中画出以AB为斜边的直角三角形ABC,点C在小正方形的顶点上,且![]() ;
;
(2)在图2中画出以AB为一边的等腰三角形ABD,点D在小正方形的顶点上,且![]() 的面积为16.
的面积为16.
查看答案和解析>>
科目:初中数学 来源: 题型:
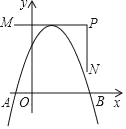
【题目】如图,抛物线y=ax2+bx+c与x轴相交于A、B两点,点A在点B左侧,顶点在折线M﹣P﹣N上移动,它们的坐标分别为M(﹣1,4)、P(3,4)、N(3,1).若在抛物线移动过程中,点A横坐标的最小值为﹣3,则a﹣b+c的最小值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com