
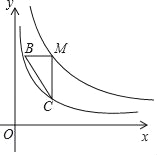
【题目】如图,点M在函数y=![]() (x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=
(x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=![]() (x>0)的图象于点B、C.
(x>0)的图象于点B、C.
(1)若点M的坐标为(1,3).
①求B、C两点的坐标;
②求直线BC的解析式;
(2)求△BMC的面积.
【答案】(1)①B(![]() ,3),C(1,1);②y=﹣3x+4;(2)
,3),C(1,1);②y=﹣3x+4;(2)![]()
【解析】(1)把点M横纵坐标分别代入![]() 解析式得到点B、C坐标,应用待定系数法求BC解析式;
解析式得到点B、C坐标,应用待定系数法求BC解析式;
(2)设出点M坐标(a,b),利用反比例函数性质,ab=3,用a、b表示BM、MC,求△BMC的面积.
(1)①∵点M的坐标为(1,3)
且B、C函数![]() (x>0)的图象上
(x>0)的图象上
∴点C横坐标为1,纵坐标为1,
点B纵坐标为3,横坐标为![]()
∴点C坐标为(1,1),点B坐标为![]()
②设直线BC解析式为![]()
把B、C点坐标代入得
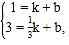
解得
![]()
∴直线BC解析式为:![]()
(2)设点M坐标为(a,b),
∵点M在函数![]() (x>0)的图象上
(x>0)的图象上
∴ab=3
由(1)点C坐标为![]() B点坐标为
B点坐标为![]()
∴![]()
∴![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)则样本容量容量是______________,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x+1的图象上的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线![]() 交x轴于点
交x轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ;
;
(1)求抛物线的解析式;
(2)点![]() 从点A出发,以1个单位/秒的速度向终点
从点A出发,以1个单位/秒的速度向终点![]() 运动,同时点
运动,同时点![]() 从点C出发,以相同的速度沿
从点C出发,以相同的速度沿![]() 轴正方向向上运动,运动的时间为
轴正方向向上运动,运动的时间为![]() 秒,当点
秒,当点![]() 到达点
到达点![]() 时,点
时,点![]() 也停止运动,设
也停止运动,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 间的函数关系式并直接写出
间的函数关系式并直接写出![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,当点![]() 在线段
在线段![]() 上时,设
上时,设![]() 交直线
交直线![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为⊙
为⊙![]() 的直径,点
的直径,点![]() ,
,![]() 是位于
是位于![]() 两侧的半圆
两侧的半圆![]() 上的动点,射线
上的动点,射线![]() 切⊙
切⊙![]() 于点
于点![]() .连接
.连接![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 是射线
是射线![]() 上一动点,连接
上一动点,连接![]() ,
,![]() ,且
,且![]() .
.
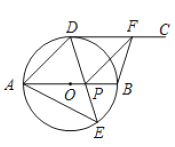
(1)求证:![]() ;
;
(2)填空:
①若![]() ,当
,当![]() __________时,四边形
__________时,四边形![]() 是菱形;
是菱形;
②若![]() ,当
,当![]() _________时,四边形
_________时,四边形![]() 是正方形。
是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自我省深化课程改革以来,某校开设了:A.利用影长求物体高度,B.制作视力表,C.设计遮阳棚,D.制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.
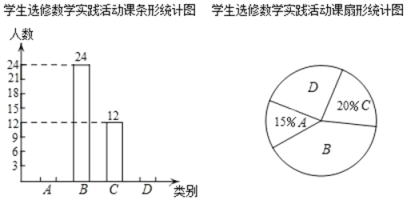
根据图中信息解决下列问题:
(1)本次共调查名学生,扇形统计图中B所对应的扇形的圆心角为度;
(2)补全条形统计图;
(3)选修D类数学实践活动的学生中有2名女生和2名男生表现出色,现从4人中随机抽取2人做校报设计,请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
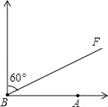
【题目】如图,A城气象台测得台风中心在A城的正西方300千米处,以每小时10![]() 千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域.
千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域.
(1)问A城是否会受到这次台风的影响?为什么?
(2)若A城受到这次台风的影响,那么A城遭受这次台风影响的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村在推进美丽乡村活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调査.获取信息如下:
购买数量低于5000块 | 购买数量不低于5000块 | |
红色地砖 | 原价销售 | 以八折销售 |
蓝色地砖 | 原价销售 | 以九折销售 |
如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.
(1)红色地砖与蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖12000块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过6000块,如何购买付款最少?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com