
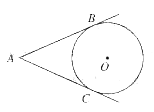
【题目】如图,![]() 、
、![]() 与
与![]() 相切于点
相切于点![]() 、
、![]() ,
,![]() ,
,![]() 为
为![]() 上异于
上异于![]() 、
、![]() 的一个动点,则
的一个动点,则![]() 的度数为( )
的度数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 或
或![]()
【答案】D
【解析】
此题分为两种情况,如图p点的位置有两个,所以∠BPC可能是锐角,也有可能是钝角,分别连接OC;OB;BP1;BP2;CP1;CP2各点
(1)当∠BPC为锐角,也就是∠BP1C时,根据AB,AC与⊙O相切,结合已知条件,在△ABC中,即可得出圆心角∠COB的度数,根据同弧所对的圆周角为圆心角的一半,即可得出∠BP1C的度数(2)如果当∠BPC为钝角,也就是∠BP2C时,根据⊙O的内接四边形的性质,即可得出∠BP2C的度数.
分别连接OC;OB;BP1;BP2;CP1;CP2各点
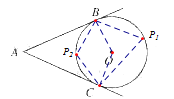
(1)当∠BPC为锐角,也就是∠BP1C时:
∵AB,AC与⊙O相切于点B,C两点
∴OC⊥AC,OB⊥AB,
∵∠A=50![]() ,
,
∴在△ABC中,∠COB=130![]() ,
,
∵在⊙O中,∠BP1C为圆周角,
∴∠BP1C=65![]() ,
,
(2)如果当∠BPC为钝角,也就是∠BP2C时
∵四边形BP1CP2为⊙O的内接四边形,
∵∠BP1C=65![]() ,
,
∴∠BP2C=115![]() ,
,
故选:D.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的2倍,则这个矩形是给定矩形的“加倍”矩形.如图,矩形![]() 是矩形
是矩形![]() 的“加倍”矩形.
的“加倍”矩形.
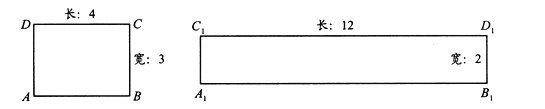
解决问题:
(1)当矩形的长和宽分别为3,2时,它是否存在“加倍”矩形?若存在,求出“加倍”矩形的长与宽,若不存在,请说明理由.
(2)边长为![]() 的正方形存在“加倍”正方形吗?请做出判断,并说明理由.
的正方形存在“加倍”正方形吗?请做出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
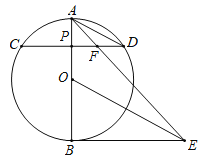
【题目】如图,AB为⊙O直径,P点为半径OA上异于O点和A点的一个点,过P点作与直径AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD交BE于E点,连接AE、DE、AE交CD于F点.
(1)求证:DE为⊙O切线;
(2)若⊙O的半径为3,sin∠ADP=![]() ,求AD;
,求AD;
(3)请猜想PF与FD的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用2700元购进甲、乙两种商品共100件,这两种商品的进价、标价如下表所示:
| 甲种 | 乙种 |
进价(元/件) | 15 | 35 |
标价(元/件) | 20 | 45 |
(1)求购进两种商品各多少件?
(2)商品将两种商品全部卖出后,获得的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
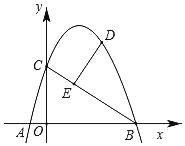
【题目】如图,抛物线y=ax2+bx+c经过A(﹣1,0)、B(4,0)、C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于点E.
(1)求抛物线的函数表达式;
(2)求线段DE长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
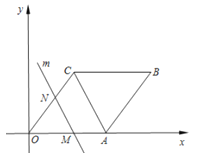
【题目】如图在平面直角坐标系中,四边形![]() 是菱形,点
是菱形,点![]() 的坐标为
的坐标为![]() ,平行于对角线
,平行于对角线![]() 的直线
的直线![]() 从原点
从原点![]() 出发,沿
出发,沿![]() 轴正方向以每秒1个单位长度的速度运动,设直线
轴正方向以每秒1个单位长度的速度运动,设直线![]() 与菱形
与菱形![]() 的两边分别交于点
的两边分别交于点![]() 、
、![]() ,直线
,直线![]() 运动的时间为
运动的时间为![]() (秒).
(秒).
(1)求点![]() 的坐标;
的坐标;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数表达式,并确定
的函数表达式,并确定![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
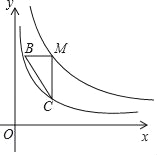
【题目】如图,点M在函数y=![]() (x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=
(x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=![]() (x>0)的图象于点B、C.
(x>0)的图象于点B、C.
(1)若点M的坐标为(1,3).
①求B、C两点的坐标;
②求直线BC的解析式;
(2)求△BMC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com