
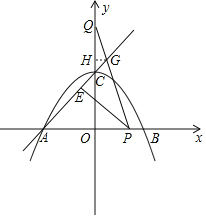
【题目】如图抛物线![]() 交x轴于点
交x轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ;
;
(1)求抛物线的解析式;
(2)点![]() 从点A出发,以1个单位/秒的速度向终点
从点A出发,以1个单位/秒的速度向终点![]() 运动,同时点
运动,同时点![]() 从点C出发,以相同的速度沿
从点C出发,以相同的速度沿![]() 轴正方向向上运动,运动的时间为
轴正方向向上运动,运动的时间为![]() 秒,当点
秒,当点![]() 到达点
到达点![]() 时,点
时,点![]() 也停止运动,设
也停止运动,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 间的函数关系式并直接写出
间的函数关系式并直接写出![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,当点![]() 在线段
在线段![]() 上时,设
上时,设![]() 交直线
交直线![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() (0<t<2),
(0<t<2),![]() (2<t≤4);(3)
(2<t≤4);(3)![]() .
.
【解析】
(1)把A点坐标代入二次函数,解得a=-![]() ,即可求解;
,即可求解;
(2)利用S=![]() CQOP,分0<t<2、2<t≤4两种情况求解即可;
CQOP,分0<t<2、2<t≤4两种情况求解即可;
(3)过点G作GH⊥y轴,利用HG∥OP,得![]() ,求出GH=
,求出GH=![]() ,利用GE=EC+CG= AC-AE+GC即可求解.
,利用GE=EC+CG= AC-AE+GC即可求解.
解:(1)把A点坐标代入二次函数,解得a=-![]() ,
,
故:二次函数的表达式为:y=-![]() x2+2;
x2+2;
(2)S=![]() CQOP,
CQOP,
当0<t<2时,
S=![]() t(-t+2)=-
t(-t+2)=-![]() t2+t,
t2+t,
当2<t≤4时,
S=![]() t(t-2)=
t(t-2)=![]() t2-t;
t2-t;
(3)t秒时,AP=t,OP=t-2,CQ=t,
直线AC与x轴的夹角为45度,
则AE=![]() ,GC=
,GC=![]() GH,AC=
GH,AC=![]() ,HC=HG,
,HC=HG,
过点G作GH⊥y轴,交y轴于点H,
∵HG∥OP,
∴![]() ,
,
即:![]() ,
,
解得:GH=![]() ,
,
则:GC=![]() GH=
GH=![]() ,
,
GE=EC+CG=AC-AE+GC=![]() .
.


科目:初中数学 来源: 题型:
【题目】某校两次购买足球和篮球的支出情况如表:
足球(个) | 篮球(个) | 总支出(元) | |
第一次 | 2 | 3 | 310 |
第二次 | 5 | 2 | 500 |
(1)求购买一个足球、一个篮球的花费各需多少元?(请列方程组求解)
(2)学校准备给帮扶的贫困学校送足球、篮球共计60个,恰逢市场对两种球的价格进行了调整,足球售价提高了10%,篮球售价降低了10%,如果要求一次性购得这批球的总费用不超过4000元,那么最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
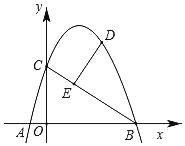
【题目】如图,抛物线y=ax2+bx+c经过A(﹣1,0)、B(4,0)、C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于点E.
(1)求抛物线的函数表达式;
(2)求线段DE长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,四边形![]() 是菱形,点
是菱形,点![]() 的坐标为
的坐标为![]() ,平行于对角线
,平行于对角线![]() 的直线
的直线![]() 从原点
从原点![]() 出发,沿
出发,沿![]() 轴正方向以每秒1个单位长度的速度运动,设直线
轴正方向以每秒1个单位长度的速度运动,设直线![]() 与菱形
与菱形![]() 的两边分别交于点
的两边分别交于点![]() 、
、![]() ,直线
,直线![]() 运动的时间为
运动的时间为![]() (秒).
(秒).
(1)求点![]() 的坐标;
的坐标;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数表达式,并确定
的函数表达式,并确定![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
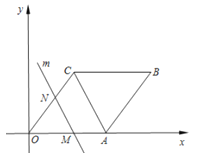
【题目】如图在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(3,4),平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与菱形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).

(1)求点B的坐标;
(2)当MN=![]() AC时,求t的值;
AC时,求t的值;
(3)设△OMN的面积为S,求S与t的函数表达式,并确定S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
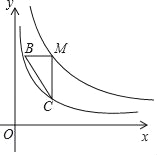
【题目】如图,点M在函数y=![]() (x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=
(x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=![]() (x>0)的图象于点B、C.
(x>0)的图象于点B、C.
(1)若点M的坐标为(1,3).
①求B、C两点的坐标;
②求直线BC的解析式;
(2)求△BMC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() .将圆心角相等的但半径不等的两个扇形
.将圆心角相等的但半径不等的两个扇形![]() 用与
用与![]() 叠合在一起,弧
叠合在一起,弧![]() 、
、![]() 、弧
、弧![]() 、
、![]() 合成了一个曲边梯形,若弧
合成了一个曲边梯形,若弧![]() 、弧
、弧![]() 的长为
的长为![]() ,
,![]() ,
,![]() .
.
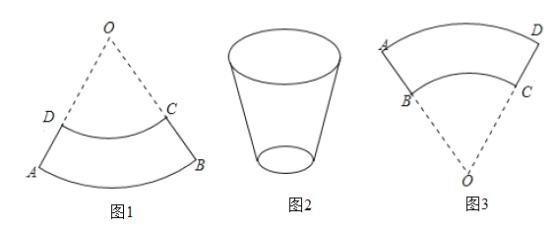
(1)试说明;曲边梯形的面积![]()
(2)某班兴趣小组进行了一次纸杯制作与探究活动.如图![]() 所示,所要制作的纸杯规格要求:杯口直径为
所示,所要制作的纸杯规格要求:杯口直径为![]() ,杯底直径为
,杯底直径为![]() ,杯壁母线为
,杯壁母线为![]() ,并且在制作过程中纸杯的侧面展开图不允许有拼接.请你求侧面展开图中弧
,并且在制作过程中纸杯的侧面展开图不允许有拼接.请你求侧面展开图中弧![]() 所在的圆的半径长度;
所在的圆的半径长度;
(3)若用一张矩形纸片,按图![]() 的方式剪裁(2)中纸杯的侧面,求这个矩形纸片的长与宽.
的方式剪裁(2)中纸杯的侧面,求这个矩形纸片的长与宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(m-1)x2-x-2=0,
(1)若x=-1是方程的一个根,求m的值及另一个根;
(2)当m为何值时方程有两个不同的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
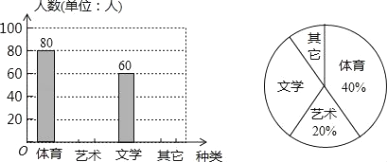
(1)此次共调查了多少人?
(2)求文学社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有1500名学生,请估计喜欢体育类社团的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com