
【题目】如图在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(3,4),平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与菱形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).

(1)求点B的坐标;
(2)当MN=![]() AC时,求t的值;
AC时,求t的值;
(3)设△OMN的面积为S,求S与t的函数表达式,并确定S的最大值.
【答案】(1)点B的坐标为(8,4);(2)![]() 或
或![]() ;(3)
;(3)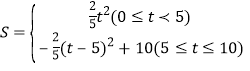 ;当t=5时,S最大值=10.
;当t=5时,S最大值=10.
【解析】
(1)过点C作CH⊥OA于H,由勾股定理求出OC,得出CB,即可得出结果;
(2)分两种情况:①当0≤t≤5时,由菱形的性质得出OA=AB=BC=OC=5,OC∥AB.由平行线得出△OMN∽△OAC,得出比例式求出OM即可;
②当5≤t≤10时,设直线MN与OA交于点E.同①可得AM=![]() .再证出△AEM∽△OAC.得出对应边成比例求出AM=AE,得出OE即可;
.再证出△AEM∽△OAC.得出对应边成比例求出AM=AE,得出OE即可;
(3)分两种情况①当0≤t<5时,求出△OAC的面积,再由相似三角形的性质得出![]() ,即可得出结果;
,即可得出结果;
②当5≤t≤10时,过点M作MT⊥x轴于T,由△BMN∽△AME可知,MT=![]() (t﹣5),得出S△OMN=S△ONE﹣S△OME=
(t﹣5),得出S△OMN=S△ONE﹣S△OME=![]() 即可得出结果.
即可得出结果.
解:(1)过点C作CH⊥OA于H,如图1所示:
∵C (3,4),
∴CH=4,OH=3,
∴![]()
∵四边形OABC是菱形,
∴CB=OC=5,5+3=8,
∴点B的坐标为(8,4);
(2)分两种情况:
①当0≤t≤5时,
如图2所示:
∵四边形OABC是菱形,
∴OA=AB=BC=OC=5,OC∥AB.
∵MN∥AC,
∴△OMN∽△OAC,
∴![]()
∵![]()
![]()
∴![]()
∴![]()
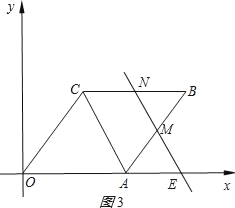
②当5≤t≤10时,如图3所示:
设直线MN与OA交于点E.,同①可得AM=![]() .
.
∵OC∥AB,MN∥AC,
∴∠COA=∠MAE,∠CAO=∠MEA,
∴△AEM∽△OAC.
∴![]()
∵OC=OA,
∴AM=AE,
∴![]()
∴![]()
综上所述:![]() 或
或![]()
(3)分两种情况:
①当0≤t<5时(如图1),![]()
∵△OMN∽△OAC,
∴![]() ,即
,即![]()
∴![]() (0≤t<5);
(0≤t<5);
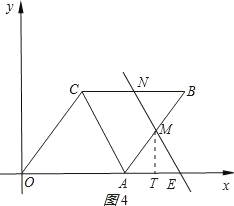
②当5≤t≤10时,过点M作MT⊥x轴于T,如图4所示:
由△BMN∽△AME可知,MT=![]() (t﹣5),
(t﹣5),
∴S△OMN=S△ONE﹣S△OME=![]()
综上所述: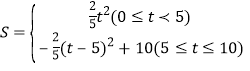
∴当t=5时,S最大值=10.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转m°得到△EDC,若点A、D、E在同一直线上,∠ACB=n°,则∠ADC的度数是( )

A. (m﹣n)°B. (90+n-![]() m)°C. (90-
m)°C. (90-![]() n+m)°D. (180﹣2n﹣m)°
n+m)°D. (180﹣2n﹣m)°
查看答案和解析>>
科目:初中数学 来源: 题型:
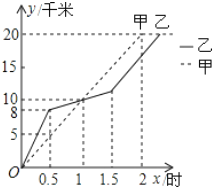
【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象
如图所示,根据图中提供的信息,有下列说法:
①两人相遇前,甲的速度小于乙的速度; ②出发后1小时,两人行程均为10km;
③出发后1.5小时,甲的行程比乙多3km; ④甲比乙先到达终点.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象
如图所示,根据图中提供的信息,有下列说法:
①两人相遇前,甲的速度小于乙的速度; ②出发后1小时,两人行程均为10km;
③出发后1.5小时,甲的行程比乙多3km; ④甲比乙先到达终点.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线![]() 交x轴于点
交x轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ;
;
(1)求抛物线的解析式;
(2)点![]() 从点A出发,以1个单位/秒的速度向终点
从点A出发,以1个单位/秒的速度向终点![]() 运动,同时点
运动,同时点![]() 从点C出发,以相同的速度沿
从点C出发,以相同的速度沿![]() 轴正方向向上运动,运动的时间为
轴正方向向上运动,运动的时间为![]() 秒,当点
秒,当点![]() 到达点
到达点![]() 时,点
时,点![]() 也停止运动,设
也停止运动,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 间的函数关系式并直接写出
间的函数关系式并直接写出![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,当点![]() 在线段
在线段![]() 上时,设
上时,设![]() 交直线
交直线![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】脱贫攻坚,让贫困群众更有幸福感,在党和政府的帮扶下,小刚家的网络商店(简称网店)将顾县豆腐干、莲桥米粉等优质土特产迅速销往全国,小刚家网店中顾县豆腐干和莲桥米粉这两种商品的相关信息如下表:
商品 | 顾县豆腐干 | 莲桥米粉 |
规格 | 1kg/袋 | 2kg/袋 |
成本(元/袋) | 20 | 19 |
售价(元/袋) | 30 | 27 |
根据上表提供的信息,解答下列问题:
(1)已知今年前五个月,小刚家网店销售上表中规格的顾县豆腐干和莲桥米粉共1500kg,获得利润1.05万元,求这前五个月小刚家网店销售这种规格的顾县豆腐干和莲桥米粉各多少袋;
(2)根据之前的销售情况,估计今年6月到10月这后五个月,小刚家网店还能销售上表中规格的顾县豆腐干和莲桥米粉共1000kg,其中,这种规格的顾县豆腐干的销售量不低于300kg.假设这后五个月,销售这种规格的顾县豆腐干x(kg),销售这种规格的顾县豆腐干和莲桥米粉获得的总利润为y(元),求出y与x之间的函数关系式,并求出这后五个月,小刚家网店销售这种规格的顾县豆腐干和莲桥米粉至少获得总利润多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,一架长4米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面所成的角为60度.
(1)求图(1)中的AO与BO的长度;
(2)若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.
①如图(2)所示,设A点下滑到C点,B点向右滑行到D点,并且AC:BD2:3,请计算AC的长度;
②如图(3)所示,当A点下滑到A点,B点向右滑行到B点时,梯子AB的中点P也随之运动到P点,若POP15,试求AA的长度.
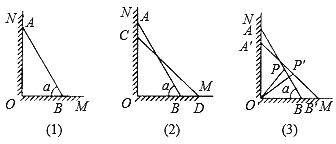
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com