【题目】脱贫攻坚，让贫困群众更有幸福感,在党和政府的帮扶下，小刚家的网络商店(简称网店)将顾县豆腐干、莲桥米粉等优质土特产迅速销往全国，小刚家网店中顾县豆腐干和莲桥米粉这两种商品的相关信息如下表：
商品 | 顾县豆腐干 | 莲桥米粉 |
规格 | 1kg/袋 | 2kg/袋 |
成本(元/袋) | 20 | 19 |
售价(元/袋) | 30 | 27 |
根据上表提供的信息，解答下列问题：
(1)已知今年前五个月，小刚家网店销售上表中规格的顾县豆腐干和莲桥米粉共1500kg，获得利润1.05万元，求这前五个月小刚家网店销售这种规格的顾县豆腐干和莲桥米粉各多少袋；
(2)根据之前的销售情况，估计今年6月到10月这后五个月，小刚家网店还能销售上表中规格的顾县豆腐干和莲桥米粉共1000kg，其中，这种规格的顾县豆腐干的销售量不低于300kg．假设这后五个月，销售这种规格的顾县豆腐干x(kg)，销售这种规格的顾县豆腐干和莲桥米粉获得的总利润为y(元)，求出y与x之间的函数关系式，并求出这后五个月，小刚家网店销售这种规格的顾县豆腐干和莲桥米粉至少获得总利润多少元．
【答案】(1)销售这种规格的顾县豆腐干750袋，销售莲桥米粉375袋；(2)至少获得总利润5800元．
【解析】
（1）设前五个月小刚家网店销售这种规格的顾县豆腐干a袋，销售莲桥米粉b袋，根据题意列方程组，解方程组即可；
（2）构建一次函数，利用一次函数的性质即可解决问题；
解：(1)设前五个月小刚家网店销售这种规格的顾县豆腐干a袋，销售莲桥米粉b袋，根据题意列方程得：a＋2b＝1500，(30－20)a＋(27－19)b＝10500，
解得：a＝750，b＝375
∴前五个月小刚家网店销售这种规格的顾县豆腐干750袋，销售莲桥米粉375袋.
(2)根据题意得：
＝
y随x的增大而增大，∵
，
∴当
时，y取得最小值，
最小值为
∴小刚家网店销售这种规格的顾县豆腐干和莲桥米粉至少获得总利润5800元．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE'F'G',此时点G'在AC上,连接CE',则CE'+CG'=______
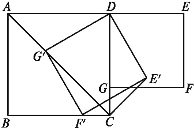
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】电视节目“奔跑吧兄弟”播出后深受中小学生的喜爱，小刚想知道大家最喜欢哪位“兄弟”，于是在本校随机抽取了一部分学生进行抽查（每人只能选一个自己最喜欢的“兄弟”），将调查结果进行了整理后绘制成如图两幅不完整的统计图，请结合图中提供的信息解答下列问题：
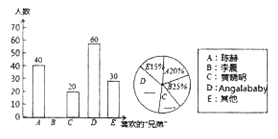
（1）本次被调查的学生有_______人.
（2）将两幅统计图补充完整.
（3）若从3名喜欢“李晨”的学生和2名喜欢“
”的学生中随机抽取两人参加文体活动，用树状图或列表法求出两人都是喜欢“李晨”的学生的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图在平面直角坐标系中，四边形OABC是菱形，点C的坐标为（3，4），平行于对角线AC的直线m从原点O出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线m与菱形OABC的两边分别交于点M、N，直线m运动的时间为t（秒）．
（1）求点B的坐标；
（2）当MN＝
AC时，求t的值；
（3）设△OMN的面积为S，求S与t的函数表达式，并确定S的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】广安市红色旅游资源丰富，无论是小平故里行，还是华蓥山上游，都吸引了不少游客。2014~2018年旅游收入不断增长，同比增速分别为：17.3%，14.7%，17.3%，16.5%，19.1%，关于这组数据，下列说法正确的是( ).
A. 中位数是14.7%B. 众数是17.3%
C. 平均数是17.98%D. 方差是0
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图
.将圆心角相等的但半径不等的两个扇形
用与
叠合在一起，弧
、
、弧
、
合成了一个曲边梯形，若弧、弧的长为
，
，
.
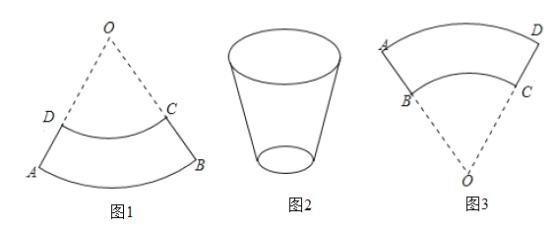
（1）试说明；曲边梯形的面积
（2）某班兴趣小组进行了一次纸杯制作与探究活动.如图
所示，所要制作的纸杯规格要求：杯口直径为
，杯底直径为
，杯壁母线为，并且在制作过程中纸杯的侧面展开图不允许有拼接.请你求侧面展开图中弧所在的圆的半径长度；
（3）若用一张矩形纸片，按图
的方式剪裁（2）中纸杯的侧面，求这个矩形纸片的长与宽.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是⊙O的内接三角形，AB是⊙O的直径，OF⊥AB，交AC于点F，点E在AB的延长线上，射线EM经过点C，且∠ACE+∠AFO=180°.
（1）求证：EM是⊙O的切线；
（2）若∠A=∠E,BC=
，求阴影部分的面积.（结果保留
和根号）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，已知抛物线y＝ax2+bx+3（a≠0）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C．
（1）求抛物线的解析式；
（2）设抛物线的对称轴与x轴交于点M，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．
（3）在（1）中抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．
（4）如图2，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．
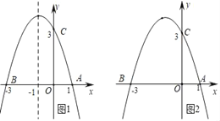
查看答案和解析>>
科目：初中数学 来源： 题型：
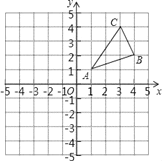
【题目】如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
（1）请画出△ABC关于原点对称的△A1B1C1，并写出点B1,C1的坐标；
（2）在x轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com