
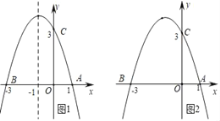
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊХзЮяЯпyЃНax2+bx+3ЃЈaЁй0ЃЉгыxжсНЛгкЕуAЃЈ1ЃЌ0ЃЉКЭЕуBЃЈЉ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшХзЮяЯпЕФЖдГЦжсгыxжсНЛгкЕуMЃЌЮЪдкЖдГЦжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїCMPЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉдкЃЈ1ЃЉжаХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕуQЃЌЪЙЕУЁїQACЕФжмГЄзюаЁЃПШєДцдкЃЌЧѓГіQЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ4ЃЉШчЭМ2ЃЌШєЕуEЮЊЕкЖўЯѓЯоХзЮяЯпЩЯвЛЖЏЕуЃЌСЌНгBEЁЂCEЃЌЧѓЫФБпаЮBOCEУцЛ§ЕФзюДѓжЕЃЌВЂЧѓДЫЪБEЕуЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2Љ2x+3ЃЛЃЈ2ЃЉДцдкЗћКЯЬѕМўЕФЕуPЃЌЦфзјБъЮЊPЃЈЉ1ЃЌ![]() ЃЉЛђPЃЈЉ1ЃЌЉ
ЃЉЛђPЃЈЉ1ЃЌЉ![]() ЃЉЛђPЃЈЉ1ЃЌ6ЃЉЛђPЃЈЉ1ЃЌ
ЃЉЛђPЃЈЉ1ЃЌ6ЃЉЛђPЃЈЉ1ЃЌ![]() ЃЉЃЛЃЈ3ЃЉДцдкЃЌQЃЈЉ1ЃЌ2ЃЉЃЛЃЈ4ЃЉ
ЃЉЃЛЃЈ3ЃЉДцдкЃЌQЃЈЉ1ЃЌ2ЃЉЃЛЃЈ4ЃЉ![]() ЃЌ
ЃЌ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉвбжЊХзЮяЯпЙ§AЁЂBСНЕуЃЌПЩНЋСНЕуЕФзјБъДњШыХзЮяЯпЕФНтЮіЪНжаЃЌгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉПЩИљОнЃЈ1ЃЉЕФКЏЪ§НтЮіЪНЕУГіХзЮяЯпЕФЖдГЦжсЃЌвВОЭЕУГіСЫMЕуЕФзјБъЃЌгЩгкCЪЧХзЮяЯпгыyжсЕФНЛЕуЃЌвђДЫCЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЌИљОнMЁЂCЕФзјБъПЩЧѓГіCMЕФОрРыЃЎШЛКѓЗжШ§жжЧщПіНјааЬжТлЃК
ЂйЕБCPЃНPMЪБЃЌPЮЛгкCMЕФДЙжБЦНЗжЯпЩЯЃЎЧѓPЕузјБъЙиМќЪЧЧѓPЕФзнзјБъЃЌЙ§PзїPQЁЭyжсгкQЃЌШчЙћЩшPMЃНCPЃНxЃЌФЧУДжБНЧШ§НЧаЮCPQжаCPЃНxЃЌOMЕФГЄЃЌПЩИљОнMЕФзјБъЕУГіЃЌCQЃН3ЉxЃЌвђДЫПЩИљОнЙДЙЩЖЈРэЧѓГіxЕФжЕЃЌPЕуЕФКсзјБъгыMЕФКсзјБъЯрЭЌЃЌзнзјБъЮЊxЃЌгЩДЫПЩЕУГіPЕФзјБъЃЎ
ЂкЕБCMЃНMPЪБЃЌИљОнCMЕФГЄМДПЩЧѓГіPЕФзнзјБъЃЌвВОЭЕУГіСЫPЕФзјБъЃЈвЊзЂвтЗжЩЯЯТСНЕуЃЉЃЎ
ЂлЕБCMЃНCPЪБЃЌвђЮЊCЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЌФЧУДжБЯпyЃН3БиДЙжБЦНЗжPMЃЌвђДЫPЕФзнзјБъЪЧ6ЃЌгЩДЫПЩЕУГіPЕФзјБъЃЛ
ЃЈ3ЃЉИљОнжсЖдГЦЉзюЖЬТЗОЖЮЪЬтНтД№ЃЛ
ЃЈ4ЃЉгЩгкЫФБпаЮBOCEВЛЪЧЙцдђЕФЫФБпаЮЃЌвђДЫПЩНЋЫФБпаЮBOCEЗжИюГЩЙцдђЕФЭМаЮНјааМЦЫуЃЌЙ§EзїEFЁЭxжсгкFЃЌSЫФБпаЮBOCEЃНSЁїBFE+SЬнаЮFOCEЃЎжБНЧЬнаЮFOCEжаЃЌFOЮЊEЕФКсзјБъЕФОјЖджЕЃЌEFЮЊEЕФзнзјБъЃЌвбжЊCЕФзнзјБъЃЌОЭжЊЕРСЫOCЕФГЄЃЎдкЁїBFEжаЃЌBFЃНBOЉOFЃЌвђДЫПЩгУEЕФКсзјБъБэЪОГіBFЕФГЄЃЎШчЙћИљОнХзЮяЯпЩшГіEЕФзјБъЃЌШЛКѓДњШыЩЯУцЕФЯпЖЮжаЃЌМДПЩЕУГіЙигкЫФБпаЮBOCEЕФУцЛ§гыEЕФКсзјБъЕФКЏЪ§ЙиЯЕЪНЃЌИљОнКЏЪ§ЕФаджЪМДПЩЧѓЕУЫФБпаЮBOCEЕФзюДѓжЕМАЖдгІЕФEЕФКсзјБъЕФжЕЃЎМДПЩЧѓГіДЫЪБEЕФзјБъЃЎ
ЃЈ1ЃЉЁпХзЮяЯпyЃНax2+bx+3ЃЈaЁй0ЃЉгыxжсНЛгкЕуAЃЈ1ЃЌ0ЃЉКЭЕуBЃЈЉ3ЃЌ0ЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЎ
ЃЎ
ЁрЫљЧѓХзЮяЯпНтЮіЪНЮЊЃКyЃНЉx2Љ2x+3ЃЛ
ЃЈ2ЃЉШчД№ЭМ1ЃЌ
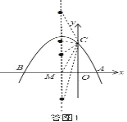
ЁпХзЮяЯпНтЮіЪНЮЊЃКyЃНЉx2Љ2x+3ЃЌ
ЁрЦфЖдГЦжсЮЊxЃН![]() ЃНЉ1ЃЌ
ЃНЉ1ЃЌ
ЁрЩшPЕузјБъЮЊЃЈЉ1ЃЌaЃЉЃЌЕБxЃН0ЪБЃЌyЃН3ЃЌ
ЁрCЃЈ0ЃЌ3ЃЉЃЌMЃЈЉ1ЃЌ0ЃЉ
ЁрЕБCPЃНPMЪБЃЌЃЈЉ1ЃЉ2+ЃЈ3ЉaЃЉ2ЃНa2ЃЌНтЕУaЃН![]() ЃЌ
ЃЌ
ЁрPЕузјБъЮЊЃКP1ЃЈЉ1ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЁрЕБCMЃНPMЪБЃЌЃЈЉ1ЃЉ2+32ЃНa2ЃЌНтЕУaЃНЁР![]() ЃЌ
ЃЌ
ЁрPЕузјБъЮЊЃКP2ЃЈЉ1ЃЌ![]() ЃЉЛђP3ЃЈЉ1ЃЌЉ
ЃЉЛђP3ЃЈЉ1ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
ЁрЕБCMЃНCPЪБЃЌгЩЙДЙЩЖЈРэЕУЃКЃЈЉ1ЃЉ2+32ЃНЃЈЉ1ЃЉ2+ЃЈ3ЉaЃЉ2ЃЌНтЕУaЃН6ЃЌ
ЁрPЕузјБъЮЊЃКP4ЃЈЉ1ЃЌ6ЃЉЃЎ
злЩЯЫљЪіДцдкЗћКЯЬѕМўЕФЕуPЃЌЦфзјБъЮЊPЃЈЉ1ЃЌ![]() ЃЉЛђPЃЈЉ1ЃЌЉ
ЃЉЛђPЃЈЉ1ЃЌЉ![]() ЃЉЛђPЃЈЉ1ЃЌ6ЃЉЛђPЃЈЉ1ЃЌ
ЃЉЛђPЃЈЉ1ЃЌ6ЃЉЛђPЃЈЉ1ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉДцдкЃЌQЃЈЉ1ЃЌ2ЃЉЃЌРэгЩШчЯТЃК
ШчД№ЭМ2ЃЌЕуCЃЈ0ЃЌ3ЃЉЙигкЖдГЦжсxЃНЉ1ЕФЖдГЦЕуCЁфЕФзјБъЪЧЃЈЉ2ЃЌ3ЃЉЃЌСЌНгACЁфЃЌжБЯпACЁфгыЖдГЦжсЕФНЛЕуМДЮЊЕуQЃЎ
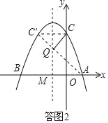
ЩшжБЯпACЁфКЏЪ§ЙиЯЕЪНЮЊЃКyЃНkx+tЃЈkЁй0ЃЉЃЎ
НЋЕуAЃЈ1ЃЌ0ЃЉЃЌCЁфЃЈЉ2ЃЌ3ЃЉДњШыЃЌЕУ![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЫљвдЃЌжБЯпACЁфКЏЪ§ЙиЯЕЪНЮЊЃКyЃНЉx+1ЃЎ
НЋxЃНЉ1ДњШыЃЌЕУyЃН2ЃЌ
МДЃКQЃЈЉ1ЃЌ2ЃЉЃЛ
ЃЈ4ЃЉЙ§ЕуEзїEFЁЭxжсгкЕуFЃЌЩшEЃЈaЃЌЉa2Љ2a+3ЃЉЃЈЉ3ЃМaЃМ0ЃЉ
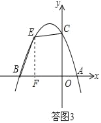
ЁрEFЃНЉa2Љ2a+3ЃЌBFЃНa+3ЃЌOFЃНЉa
ЁрSЫФБпаЮBOCEЃН![]() BFEF+
BFEF+![]() ЃЈOC+EFЃЉOF
ЃЈOC+EFЃЉOF
ЃН![]() ЃЈa+3ЃЉЃЈЉa2Љ2a+3ЃЉ+
ЃЈa+3ЃЉЃЈЉa2Љ2a+3ЃЉ+![]() ЃЈЉa2Љ2a+6ЃЉЃЈЉaЃЉ
ЃЈЉa2Љ2a+6ЃЉЃЈЉaЃЉ
ЃНЉ![]() a2Љ
a2Љ![]() a+
a+![]() ЃНЉ
ЃНЉ![]() ЃЈa+
ЃЈa+![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЁрЕБaЃНЉ![]() ЪБЃЌSЫФБпаЮBOCEзюДѓЃЌЧвзюДѓжЕЮЊ
ЪБЃЌSЫФБпаЮBOCEзюДѓЃЌЧвзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ДЫЪБЃЌЕуEзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋЁїABCШЦЕуCЫГЪБеыа§зЊmЁуЕУЕНЁїEDCЃЌШєЕуAЁЂDЁЂEдкЭЌвЛжБЯпЩЯЃЌЁЯACB=nЁуЃЌдђЁЯADCЕФЖШЪ§ЪЧЃЈЁЁЁЁЃЉ

A. ЃЈmЉnЃЉЁуB. ЃЈ90+nЃ![]() mЃЉЁуC. ЃЈ90Ѓ
mЃЉЁуC. ЃЈ90Ѓ![]() n+mЃЉЁуD. ЃЈ180Љ2nЉmЃЉЁу
n+mЃЉЁуD. ЃЈ180Љ2nЉmЃЉЁу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭбЦЖЙЅМсЃЌШУЦЖРЇШКжкИќгаавИЃИа,дкЕГКЭеўИЎЕФАяЗіЯТЃЌаЁИеМвЕФЭјТчЩЬЕъ(МђГЦЭјЕъ)НЋЙЫЯиЖЙИЏИЩЁЂСЋЧХУзЗлЕШгХжЪЭСЬиВњбИЫйЯњЭљШЋЙњЃЌаЁИеМвЭјЕъжаЙЫЯиЖЙИЏИЩКЭСЋЧХУзЗлетСНжжЩЬЦЗЕФЯрЙиаХЯЂШчЯТБэЃК
ЩЬЦЗ | ЙЫЯиЖЙИЏИЩ | СЋЧХУзЗл |
ЙцИё | 1kg/Дќ | 2kg/Дќ |
ГЩБО(дЊ/Дќ) | 20 | 19 |
ЪлМл(дЊ/Дќ) | 30 | 27 |
ИљОнЩЯБэЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
(1)вбжЊНёФъЧАЮхИідТЃЌаЁИеМвЭјЕъЯњЪлЩЯБэжаЙцИёЕФЙЫЯиЖЙИЏИЩКЭСЋЧХУзЗлЙВ1500kgЃЌЛёЕУРћШѓ1.05ЭђдЊЃЌЧѓетЧАЮхИідТаЁИеМвЭјЕъЯњЪлетжжЙцИёЕФЙЫЯиЖЙИЏИЩКЭСЋЧХУзЗлИїЖрЩйДќЃЛ
(2)ИљОнжЎЧАЕФЯњЪлЧщПіЃЌЙРМЦНёФъ6дТЕН10дТетКѓЮхИідТЃЌаЁИеМвЭјЕъЛЙФмЯњЪлЩЯБэжаЙцИёЕФЙЫЯиЖЙИЏИЩКЭСЋЧХУзЗлЙВ1000kgЃЌЦфжаЃЌетжжЙцИёЕФЙЫЯиЖЙИЏИЩЕФЯњЪлСПВЛЕЭгк300kgЃЎМйЩшетКѓЮхИідТЃЌЯњЪлетжжЙцИёЕФЙЫЯиЖЙИЏИЩx(kg)ЃЌЯњЪлетжжЙцИёЕФЙЫЯиЖЙИЏИЩКЭСЋЧХУзЗлЛёЕУЕФзмРћШѓЮЊy(дЊ)ЃЌЧѓГіyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіетКѓЮхИідТЃЌаЁИеМвЭјЕъЯњЪлетжжЙцИёЕФЙЫЯиЖЙИЏИЩКЭСЋЧХУзЗлжСЩйЛёЕУзмРћШѓЖрЩйдЊЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
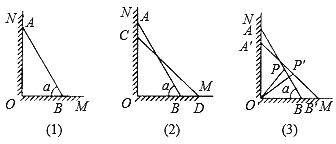
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЫљЪОЃЌвЛМмГЄ4УзЕФЬнзгABаБППдкгыЕиУцOMДЙжБЕФЧНБкONЩЯЃЌЬнзггыЕиУцЫљГЩЕФНЧЮЊ60ЖШ.
ЃЈ1ЃЉЧѓЭМЃЈ1ЃЉжаЕФAOгыBOЕФГЄЖШЃЛ
ЃЈ2ЃЉШєЬнзгЖЅЖЫAбиNOЯТЛЌЃЌЭЌЪБЕзЖЫBбиOMЯђгвЛЌаа.
ЂйШчЭМЃЈ2ЃЉЫљЪОЃЌЩшAЕуЯТЛЌЕНCЕуЃЌBЕуЯђгвЛЌааЕНDЕуЃЌВЂЧвAC:BD2:3ЃЌЧыМЦЫуACЕФГЄЖШЃЛ
ЂкШчЭМЃЈ3ЃЉЫљЪОЃЌЕБAЕуЯТЛЌЕНAЕуЃЌBЕуЯђгвЛЌааЕНBЕуЪБЃЌЬнзгABЕФжаЕуPвВЫцжЎдЫЖЏЕНPЕуЃЌШєPOP15ЃЌЪдЧѓAAЕФГЄЖШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁїABCдкЗНИёжНжаЮЛжУШчЭМЫљЪО
ЃЈ1ЃЉЧыдкЗНИёжНЩЯНЈСЂЦНУцжБНЧзјБъЯЕЃЌЪЙЕУAЁЂBСНЕуЕФзјБъЗжБ№ЮЊAЃЈ2ЃЌЉ1ЃЉЁЂBЃЈ1ЃЌЉ4ЃЉЃЌВЂЧѓГіCЕуЕФзјБъЃЛ
ЃЈ2ЃЉзїГіЁїABCЙигкКсжсЖдГЦЕФЁїA1B1C1ЃЌдйзїГіЁїABCвдзјБъдЕуЮЊа§зЊжааФЁЂа§зЊ180ЁуКѓЕФЁїA2B2C2ЃЌВЂаДC1ЃЌC2СНЕуЕФзјБъЃЛ
ЃЈ3ЃЉЙлВьЁїA1B1C1КЭЁїA2B2C2ЃЌЦфжаЕФвЛИіШ§НЧаЮФмЗёгЩСэвЛИіШ§НЧаЮОЙ§ФГжжБфЛЛЖјЕУЕНЃПШєФмЃЌЧыжИГіЪВУДБфЛЛЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
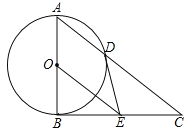
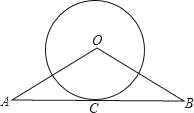
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯABCЃН90ЁуЃЌвдABЕФжаЕуOЮЊдВаФЃЌOAЮЊАыОЖЕФдВНЛACгкЕуDЃЌEЪЧBCЕФжаЕуЃЌСЌНгDEЃЌOEЃЎ
ЃЈ1ЃЉХаЖЯDEгыЁбOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЧѓжЄЃКBC2ЃН2CDOEЃЛ
ЃЈ3ЃЉШє![]() ЃЌЧѓOEЕФГЄЃЎ
ЃЌЧѓOEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаетбљвЛИіЬтФПЃК
АДееИјЖЈЕФМЦЫуГЬађЃЌШЗЖЈЪЙДњЪ§ЪНnЃЈn+2ЃЉДѓгк2000ЕФnЕФзюаЁе§ећЪ§жЕЃЎЯывЛЯыЃЌдѕбљбИЫйевЕНетИіnжЕЃЌЧыгыЭЌбЇУЧНЛСїФуЕФЬхЛсЃЎ
аЁССГЂЪдМЦЫуСЫМИзщnКЭnЃЈn+2ЃЉЕФЖдгІжЕШчЯТБэЃК
n | 50 | 40 | |
nЃЈn+2ЃЉ | 2600 | 1680 |
ЃЈ1ЃЉЧыФуМЬајаЁССЕФГЂЪдЃЌдйЫуМИзщЬюдкЩЯБэжаЃЈМИзщЫцвтЃЌздМКЛИёЃЉЃЌВЂаДГіТњзуЬтФПвЊЧѓЕФnЕФжЕЃЛ
ЃЈ2ЃЉНсКЯЩЯЪіЙ§ГЬЃЌЖдгкЁАдѕбљбИЫйевЕНnжЕЁБетИіЮЪЬтЃЌЫЕЫЕФуЕФЯыЗЈЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
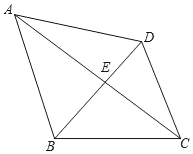
ЁОЬтФПЁПШчЭМЫљЪОЃЌЫФБпаЮABCDжаЃЌ![]() ЃЌЖдНЧЯпACЁЂBDНЛгкЕуEЃЌЧв
ЃЌЖдНЧЯпACЁЂBDНЛгкЕуEЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌдђCEЕФГЄЮЊ_____ЃЎ
ЃЌдђCEЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпABОЙ§ЁбOЩЯЕФЕуCЃЌЧвOAЃНOBЃЌCAЃНCBЃЎ
ЃЈ1ЃЉжБЯпABЪЧЁбOЕФЧаЯпТ№ЃПЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєЁбOЕФжБОЖЮЊ8cmЃЌABЃН10cmЃЌЧѓOAЕФГЄЃЎЃЈНсЙћБЃСєИљКХЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com