
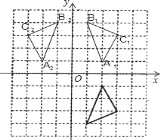
【题目】△ABC在方格纸中位置如图所示
(1)请在方格纸上建立平面直角坐标系,使得A、B两点的坐标分别为A(2,﹣1)、B(1,﹣4),并求出C点的坐标;
(2)作出△ABC关于横轴对称的△A1B1C1,再作出△ABC以坐标原点为旋转中心、旋转180°后的△A2B2C2,并写C1,C2两点的坐标;
(3)观察△A1B1C1和△A2B2C2,其中的一个三角形能否由另一个三角形经过某种变换而得到?若能,请指出什么变换.

【答案】(1))坐标系见解析,C(3,﹣3);(2)所作图形见解析,C1(3,3),C2(﹣3,3);(3)能,答案见解析.
【解析】
(1)根据已知点的坐标,画出坐标系,由坐标系确定C点坐标;
(2)由轴对称性画△A1B1C1,由关于原点中心对称性画△A2B2C2,可确定写出C1,C2两点的坐标;
(3)直接观察图中的△A1B1C1和△A2B2C2,即可得出答案.
(1)坐标系如下图所示,C(3,﹣3);
(2)△A1B1C1,△A2B2C2如下图所示,
其中C1,C2两点的坐标分别为:C1(3,3),C2(﹣3,3).
(3)△A1B1C1和△A2B2C2,其中的一个三角形能由另一个三角形经过对称变换而得到.


科目:初中数学 来源: 题型:
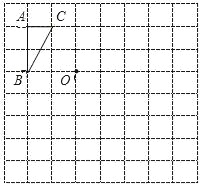
【题目】如图8×8正方形网格中,点A、B、C和O都为格点.
(1)利用位似作图的方法,以点O为位似中心,可将格点三角形ABC扩大为原来的2倍.请你在网格中完成以上的作图(点A、B、C的对应点分别用A′、B′、C′表示);
(2)当以点O为原点建立平面坐标系后,点C的坐标为(﹣1,2),则A′、B′、C′三点的坐标分别为:A′: B′: C′: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广安市红色旅游资源丰富,无论是小平故里行,还是华蓥山上游,都吸引了不少游客。2014~2018年旅游收入不断增长,同比增速分别为:17.3%,14.7%,17.3%,16.5%,19.1%,关于这组数据,下列说法正确的是( ).
A. 中位数是14.7%B. 众数是17.3%
C. 平均数是17.98%D. 方差是0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OF⊥AB,交AC于点F,点E在AB的延长线上,射线EM经过点C,且∠ACE+∠AFO=180°.
(1)求证:EM是⊙O的切线;
(2)若∠A=∠E,BC=![]() ,求阴影部分的面积.(结果保留
,求阴影部分的面积.(结果保留![]() 和根号).
和根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,给出如下定义:已知两个函数,如果对于任意的自变量x,这两个函数对应的函数值记为y1、y2,恒有点x,y1和点x,y2关于点x,x成中心对称(此三个点可以重合),由于对称中心x,x都在直线yx上,所以称这两个函数为关于直线yx的“相依函数”.例如:y3x和y5x为关于直线yx的“相依函数”
(1)已知点M1,m是直线y2x4上一点,请求出点M1,m关于点1,1成中心对称的点N的坐标;
(2)若直线y3xn和它关于直线yx的“相依函数”的图象与y轴围成的三角形的面积为8,求n的值;
(3)若二次函数yax2bxc和yx2d为关于直线yx的“相依函数”.
①请求出a、b的值;
②已知点P3,2、点Q2,2,连接PQ,直接写出yax2bxc和yx2d两条抛物线与线段PQ有且只有两个交点时对应的d的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
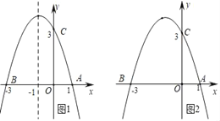
【题目】如图1,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)在(1)中抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(4)如图2,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
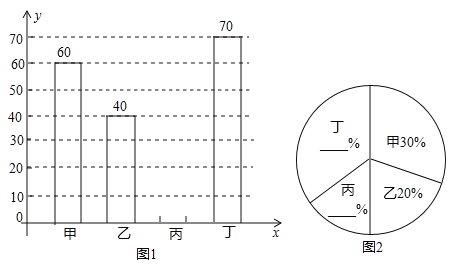
【题目】某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、丁四个班级植树的棵树和所占百分比情况进行了调查,将收集的数据整理并绘制成图1和图2两幅不完整的统计图,请根据图中的信息,完成下列问题:
(1)这四个班共植树 棵;
(2)请补全两幅统计图;
(3)若四个班级植树的平均成活率是95%,全校共植树2000棵,请你估计全校种植的树中成活的树大约有多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
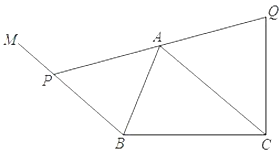
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .过点
.过点![]() 作
作![]() ,动点
,动点![]() 在射线
在射线![]() 上(点
上(点![]() 不与
不与![]() 重合),联结
重合),联结![]() 并延长到点
并延长到点![]() ,使
,使![]() .
.
(1)求![]() 的面积;
的面积;
(2)设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)连接![]() ,如果
,如果![]() 是直角三角形,求
是直角三角形,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com