
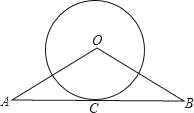
【题目】已知直线AB经过⊙O上的点C,且OA=OB,CA=CB.
(1)直线AB是⊙O的切线吗?请说明理由;
(2)若⊙O的直径为8cm,AB=10cm,求OA的长.(结果保留根号)
科目:初中数学 来源: 题型:
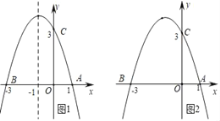
【题目】如图1,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)在(1)中抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(4)如图2,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
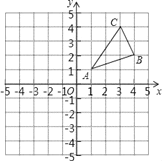
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于原点对称的△A1B1C1,并写出点B1,C1的坐标;
(2)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
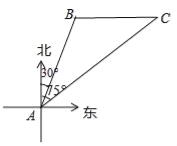
【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
![]()
![]() (参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,![]() =1.732,
=1.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
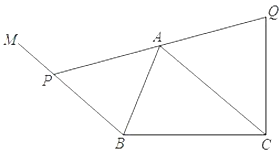
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .过点
.过点![]() 作
作![]() ,动点
,动点![]() 在射线
在射线![]() 上(点
上(点![]() 不与
不与![]() 重合),联结
重合),联结![]() 并延长到点
并延长到点![]() ,使
,使![]() .
.
(1)求![]() 的面积;
的面积;
(2)设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)连接![]() ,如果
,如果![]() 是直角三角形,求
是直角三角形,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,两个全等的△ABC和△DEF中,∠ACB=∠DFE=90°,AB=DE,其中点B和点D重合,点F在BC上,将△DEF沿射线BC平移,设平移的距离为x,平移后的图形与△ABC重合部分的面积为y,y关于x的函数图象如图2所示(其中0≤x≤m,m<x≤3,3<x≤4时,函数的解析式不同)
(1)填空:BC的长为_____;
(2)求y关于x的函数关系式,并写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “掷一枚硬币正面朝上的概率是![]() ”表示每抛硬币2次就有1次正面朝上
”表示每抛硬币2次就有1次正面朝上
B. 一组数据2,2,3,6的众数和中位数都是2
C. 要了解全市人民的低碳生活状况,适宜采用抽样调查的方法
D. 随机抽取甲、乙两名同学的5次数学成绩,计算得平均分都是90分,方差分别是S2甲=5,S2乙=12,说明乙的成绩较为稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
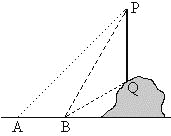
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).备用数据:![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com